第三章：静磁场VIP免费

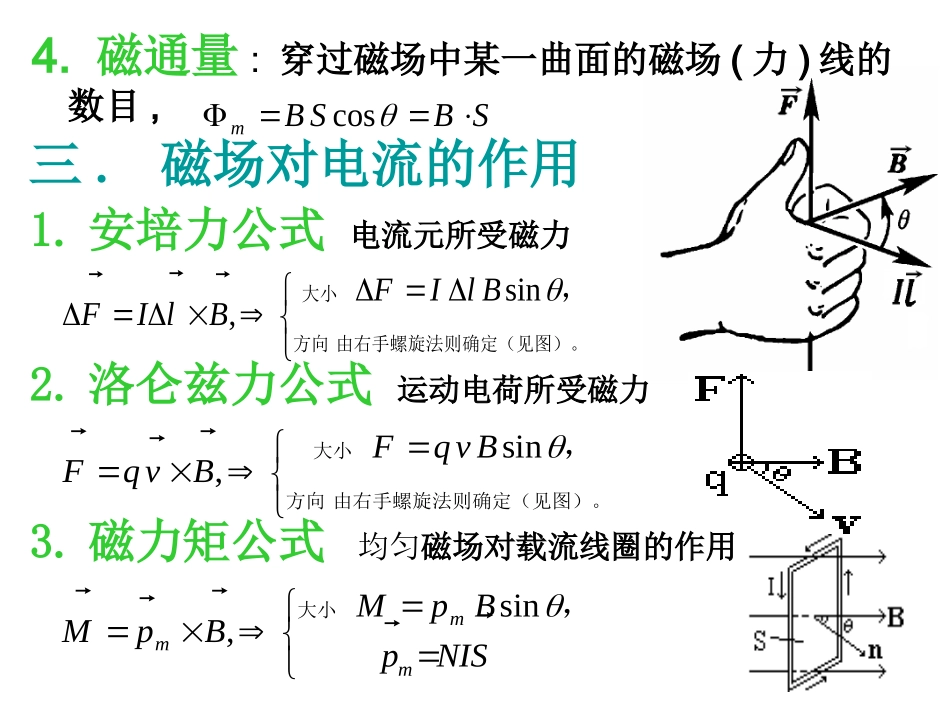
第三章:静磁场一.磁场的概念电流的磁场磁场线1、磁性的根源:电流→(激发)磁场(作用)→电流2.磁场的性质:涡(有)旋场,无源(散)场3.磁场(力)线:无头无尾的,不相交不中断的二.磁感应强度B磁通量1.B的定义:电流元Idl,在磁场中受最大磁力为dFmax,定义：的大小为的方向为:沿Idl受力为零时Idl的方位,或2.毕奥—萨伐尔定律:电流元激发磁场3.几种常见电流分布的磁场:a.圆电流在其轴上的磁场:b.无限长载流直导线的磁场:c.无限长载流圆柱体的磁场:d.无限长载流直螺线管内的磁场:304drrlIBdRIRzIBB20在圆圆心)(202/3220,rIRrIBRrBRr20柱外2020)(,)(柱内rIB20nIB0BBlIFddlIFBddmaxB4.磁通量:穿过磁场中某一曲面的磁场(力)线的数目,三.磁场对电流的作用1.安培力公式电流元所受磁力2.洛仑兹力公式运动电荷所受磁力3.磁力矩公式均匀磁场对载流线圈的作用SBSBmcos确定（见图）。大小，由右手螺旋法则方向sin,BlIFBlIF（见图）。法大小，则确定由右手螺旋方向sin,BvqFBvqFSNIpBpMBpMmmm，大小sin,四.带电粒子在电磁场中的运动1.在均匀磁场中(1)v0∥B的情形:F=0,匀速直线运动(2)v0⊥B的情形:(3)v0与B成θ角的情形:平行B方向上作匀速直线运动；垂直B方向上作匀速圆周运动；合成运动:螺旋线运动2.在电场磁场均存在的空间:结合牛顿力学,讨论粒子的运动.cos,sin,0//000//000vvvvvvv匀速圆周运动,2rvmvBqFqBmvqBmqBmvhTrcos220,,螺距周期半径与速度无关周期半径,,2qBmqBmvTr),(BvEqF五、例题例1:顶点向上,顶角为2θ的圆锥放在水平面上,空间存在竖直向下的均匀磁场B,今有一质量为m,电荷为q的小球在光滑的锥面上作匀速圆周运动,试求小球圆运动的最小半径.解:依题意小球的圆轨迹应在水平面内,圆心应在锥面的轴线上,设其速度为v,半径为R,由受力分析有方程0tanc2gRvvmqBRmgNmqvBNRvsin,cos2分量式RvLLaqvBFamgmNF2,,2222)(tanc4min2tanc4)(qBgmmgRmqBRqBRRv由实解条件，得例2:电子在电子枪内经U0=103V的电压加速后从枪口水平射出,在偏离出口速度方向θ=60°,且距枪口O处s=50cm的M点有一靶子,为使电子能击中靶子现施加强度不超过B<0.003T的均匀磁场,问:(1)当垂直纸面施加,(2)平行OM方向施加时,实验者实际采用的磁场如何？解：(1)B的方向只能向里，电子出口速度为电子在磁场中会做圆周运动,O、M是该圆周上的两点,圆心设在O点下方的O’点,其半径R可由△OMO’的几何关系计算为只有一种选择meUmvveU02220,,3sin2/ssR)(103)(107.334620TTBsemU,eBmvR又解:(2)由于电子出口速度与磁场有夹角,所以电子将作螺旋线运动,要击中靶,则要求螺距h满足s=kh,k=1,2,…而所以即,平行OM方向施加磁场时,为击中靶子,实验者可有四种磁场量值的选择.,cos2//qBvmTvh),(107.64cos2TkkBqsvm),(100.3),(1068.2),(1001.2),(1034.1),(107.6:(54321:33334TTTTTBk不合题意）例3:在空间有相互垂直的均匀电场E和磁场B(如图所示),一电子从原点静止释放,求它在y轴方向前进的最大距离.解:设电子在y轴前进到达最大距离ym时的速度为v(沿x轴方向，为什么？),由动能定理有(洛仑兹力不做功)，电场力方向沿y轴,故电子沿x轴的速度增量应归因于洛仑兹力f,设水平分量的平均值为,则由动量定理，沿x方向有其中解得,22mvmeEy,mvtfxxf,,myyxytvveBf,22eBEmmy例4:在真空建立如图所示坐标系,在0≤y≤L的区域内有均匀磁场B,方向沿z轴正向(向里).荷质比为q/m的带正电粒子由x=0,y=-h,z=0处静止释放,粒子下落过原点的时刻开始计时,求粒子在磁场中任一时刻t的位置和它离开磁场时的位置、速度.解:第一段,粒子由静止下落至原点,速度为第二段,粒子进入磁场后在重力和洛仑兹力的作用下作初速为v1的曲线运动,洛仑兹力的大小和方向都是变化的,一般解析分析可能会复杂化。现在我们作这样的设想:在原点...