282解直角三角形1VIP免费

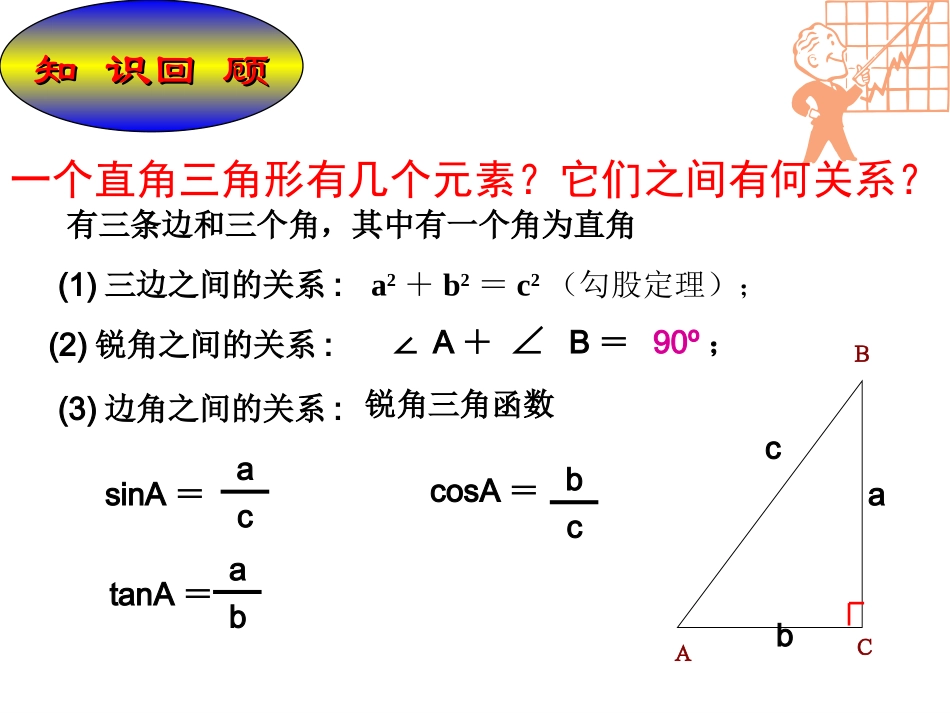
知识回顾知识回顾一个直角三角形有几个元素？它们之间有何关系？(1)三边之间的关系:a2＋b2＝c2（勾股定理）；(2)锐角之间的关系:∠A＋∠B＝90º；(3)边角之间的关系:sinA＝accosA＝tanA＝ＡＣＢabc有三条边和三个角，其中有一个角为直角bcab锐角三角函数复习30°、45°、60°角的正弦值、余弦值和正切值如下表：锐角a三角函数30°45°60°sinacosatana1222322212332331对于sinα与tanα，角度越大，函数值也越大；（带正）对于cosα，角度越大，函数值越小。在直角三角形中，除直角外，还有哪些元素?这5个元素之间有什么关系?知道其中哪些元素，可以求出其余的元素?cbaCBA在RtABC△中,（1）根据∠A=60°,斜边AB=30,你能求出这三个角的其他元素吗？A在直角三角形的六个元素中,除直角外,如果知道两个元素,就可以求出其余三个元素.(其中至少有一个是边),你发现了什么BC∠BACBC6∠A∠BAB一角一边两边2（2）根据AC=，BC=你能求出这个三角形的其他元素吗？26两角（3）根∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?不能在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形解直角三角形的依据ＡＣＢabc(1)三边之间的关系:a2＋b2＝c2（勾股定理）；(2)锐角之间的关系:∠A＋∠B＝90º；(3)边角之间的关系:tanA＝absinA＝accosA＝bc新知识新知识（4）面积公式：hcbaSABC2121▲例题分析1.在RtABC△中,C=90°,AC=,BC∠=,解这个直角三角形.解：由勾股定理得：22622222BCABAB在RtABC△中，AB=2AC所以，∠B=30°A=60°∠ACBCtanA解：32660A3060-90A-90B222ACABCAB26?26例题分析2、在RtABC△中，∠C=90°，∠B=60°,b=.解这个直角三角形.CBA3434解：在RtABC△中，∠B=60°,b=∴∠A=30°,c=2a34方法一：设a=x，c=2x由勾股定理得：222342xx)(舍去或解得：44xx∴c=8，a=4方法二：baAtan即：3403tana3433a4a解得：∴c=8方法一方法二比较这两种方法哪个方法更简单？基础练习1、在下列直角三角形中不能求解的是（）A、已知一直角边一锐角B、已知一斜边一锐角C、已知两边D、已知两角2、RtABC△中，∠C=90°,若sinA=，AB=10，那么BC=_____，tanB=______．D45843基础练习3.在RtABC△中,C=90°∠，a、b、c分别为∠A、∠B、∠C的对边.根据已知条件，解直角三角形.(1)c=8，∠A=60°；(4)a=1，∠B=30°.(2)b=，c=4；22(3)a=，b=6；23例题分析3.如图，在Rt△ABC中，∠C＝90°，AC=6，∠BAC的平分线AD=，解这个直角三角形。34DABC643解：63cos243ACCADAD30CAD因为AD平分∠BAC60,30CABB12,63ABBC例4:如图，在△ABC中，∠B=45°，∠C=30°，AB=，求AC和BC。24尝试一下:你还有其它方法吗？请同学们试着用这两种方法做做看。(小组合作)例4:如图，在△ABC中，∠B=45°，∠C=30°，AB=，求AC和BC。24在⊿ABC中，∠C=900，解直角三角形：(如图)CAB4.已知a,c.则通过，求∠A1.已知∠A，a.则b=c=a3.已知∠A，b.则a=的2.已知∠A，c.则a=b=a提高练习5.已知b,c.则通过，求∠AAatanAasinAcsinAccosAtanbcaAsincbAcos解直角三角形∠A＋∠B＝90°a2+b2=c2三角函数关系式sin,sinabABcccos,cosbaAAcctan,tanabABba归纳小结解直角三角形：由已知元素求未知元素的过程直角三角形中，AB∠A的对边aC∠A的邻边b┌斜边c已知一边一角如何解直角三角形？