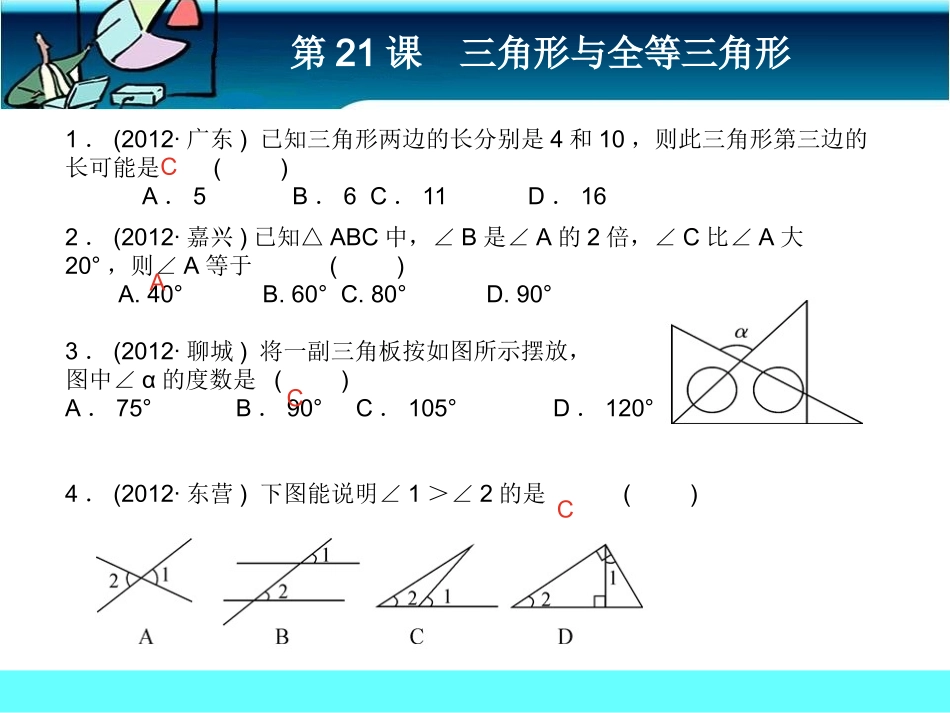
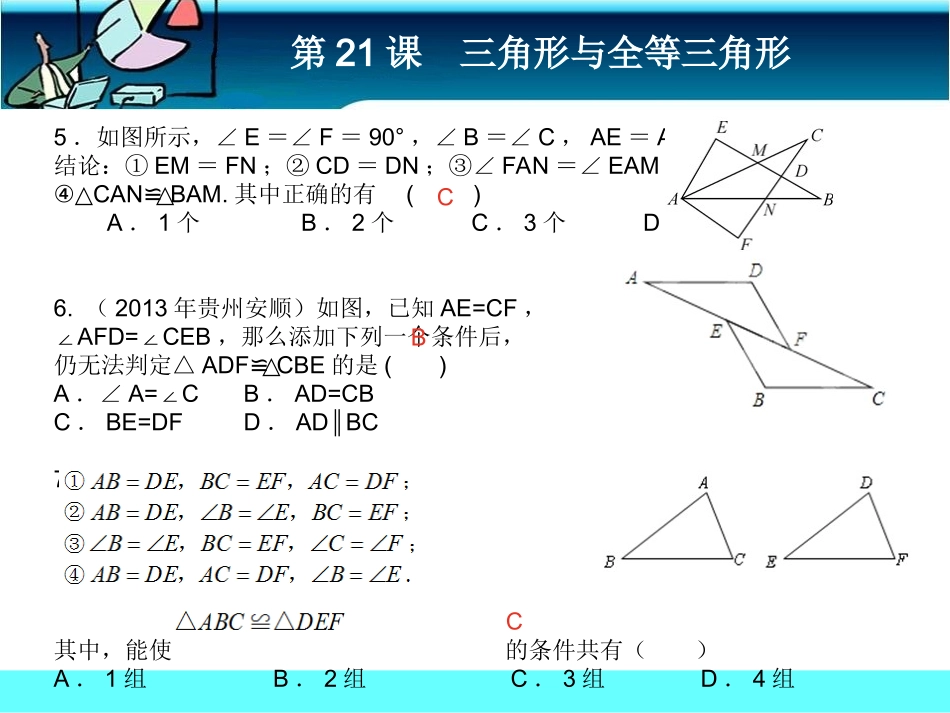
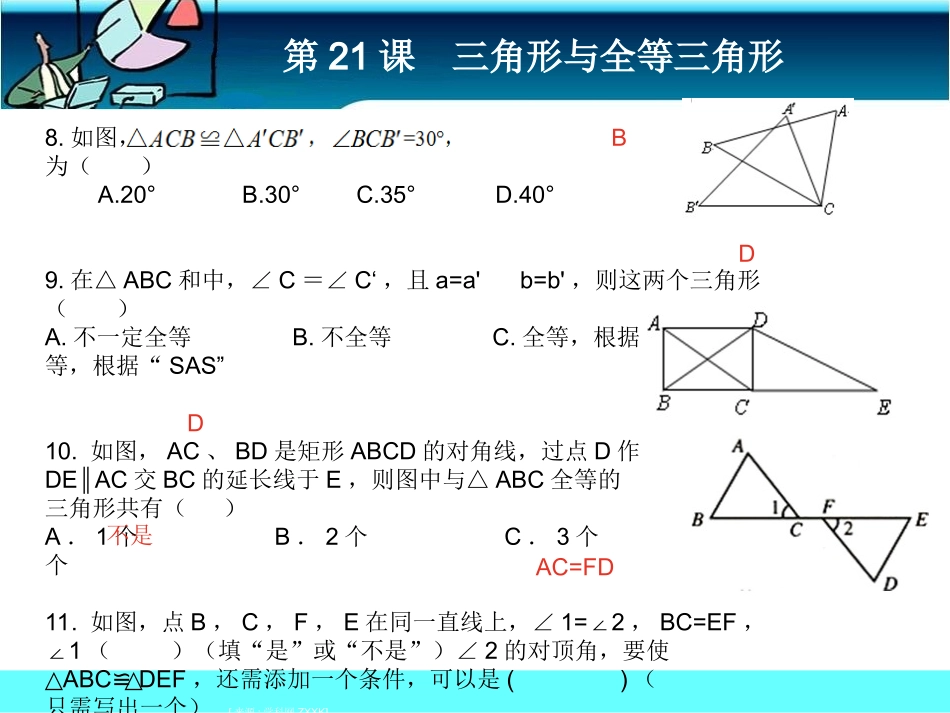
第21课三角形与全等三角形1.(2012·广东)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是()A.5B.6C.11D.162.(2012·嘉兴)已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于()A.40°B.60°C.80°D.90°3.(2012·聊城)将一副三角板按如图所示摆放,图中∠α的度数是()A.75°B.90°C.105°D.120°4.(2012·东营)下图能说明∠1>∠2的是()ACCC第21课三角形与全等三角形5.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△CANBAM.≌△其中正确的有()A.1个B.2个C.3个D.4个6.(2013年贵州安顺)如图,已知AE=CF,∠AFD=CEB∠,那么添加下列一个条件后,仍无法判定△ADFCBE≌△的是()A.∠A=C∠B.AD=CBC.BE=DFD.ADBC∥7.如图,给出下列四组条件:其中,能使的条件共有()A.1组B.2组C.3组D.4组CBC第21课三角形与全等三角形8.如图,则的度数为()A.20°B.30°C.35°D.40°9.在△ABC和中,∠C=∠C‘,且a=a'b=b',则这两个三角形()A.不一定全等B.不全等C.全等,根据“ASA”D.全等,根据“SAS”10.如图,AC、BD是矩形ABCD的对角线,过点D作DEAC∥交BC的延长线于E,则图中与△ABC全等的三角形共有()A.1个B.2个C.3个D.4个11.如图,点B,C,F,E在同一直线上,∠1=2∠,BC=EF,∠1()(填“是”或“不是”)∠2的对顶角,要使△ABCDEF≌△,还需添加一个条件,可以是()(只需写出一个)[来源:学科网ZXXK]DBD不是AC=FD第21课三角形与全等三角形13.(2013•湘西州)如图,在▱ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是()14.(2013•娄底)如图,AB=AC,要使△ABEACD≌△,应添加的条件是()(添加一个条件即可).∠B=C∠或AE=AD1:230°第21课三角形与全等三角形15.(2013•郴州)如图,点D、E分别在线段AB,AC上,AE=AD,不添加新的线段和字母,要使△ABEACD≌△,需添加的一个条件是()(答案不唯一)(只写一个条件即可).16.(2013•白银)如图,已知BC=EC,∠BCE=ACD∠,要使△ABCDEC≌△,则应添加的一个条件为().(答案不唯一,只需填一个)[来源:学科网ZXXK]AC=CD∠B=C∠