三角形的内角和与三角形的外角VIP免费

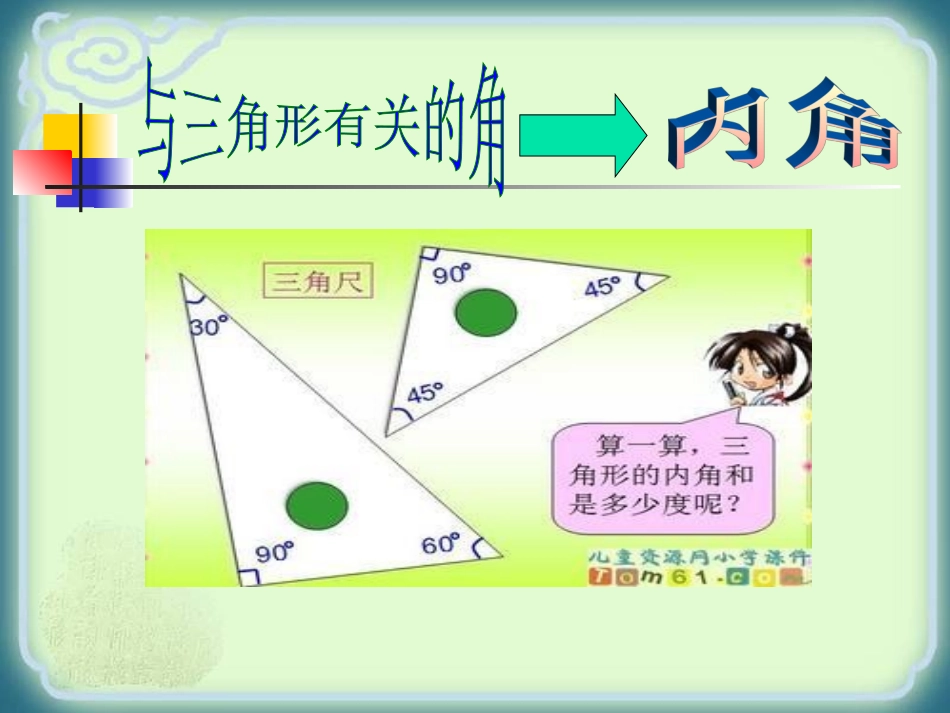
证明：将ΔABC的边BC所在的直线平移，使其像经过点A，得到直线B'C'B’C’已知：ΔABC（图3-1）求证：∠A+∠B+∠C=1800CAB内角和定理：三角形的内角和等于180。∵BC∥B'C'∴∠BAB'=∠B∠C'AC=∠C（两直线平行，内错角相等）∵∠BAB'+∠BAC+∠C'AC=1800（平角的定义）∴∠B+∠BAC+∠C=1800在ΔABC中，∠A的度数是∠B的度数的3倍，∠C比∠B大15,求∠A，∠B，∠C的度数。解：设∠B为,则∠A为，∠C为所以x(3)x(15)x3(15)180xxxx解得：=33所以399,1548xx答：∠A，∠B,∠C的度数分别为99。，33。，48。一个三角形的三个内角中，最多有几个直角？最多有几个钝角？由于三角形的内角和等于180。，因此最多有一个直角或一个钝角。锐角三角形：直角三角形：钝角三角形：锐角三角形直角三角形钝角三角形三个角都是锐角的三角形有一个角是直角的三角形，可用符号“RtΔ”来表示，如直角三角形ABC可记作“RtΔABC”有一个角是钝角的三角形外角相邻内角不相邻内角三角形的一边与另一边的延长线所组成的角，叫做三角形的外角如右图：把ΔABC的一边BC延长，得到外角∠ACD，则∠ACB是与它相邻的内角，∠A，∠B是与它不相邻的内角ABCD如图：外角∠ACD和与它不相邻的内角∠A，∠B之间有什么大小关系？证明：因为∠ACD+∠ACB=180。结论：三角形的一个外角等于和它不相邻的两个内角的和.∠A+∠B+∠ACB=180。所以∠ACD-∠A-∠B=0于是∠ACD=∠A+∠B1、已知：如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.求：∠B和∠ACB的大小.解：∵∠DCA是△ABC的一个外角(已知)∠DCA=100°，∠A=45°(已知)∴∠B=100°-45°=55°(三角形的一个外角等于和它不相邻的两个内角的和)又∵∠DCA+∠BCA=180°(平角意义)∴∠ACB=80°(等式的性质）ABCD100°45°一、选择题(1)在△ABC中，∠A:∠B:∠C=1:2:3，则∠B=（）A.300B.600C.900D.1200(2)在△ABC中，∠A=500,∠B=800,则∠C=（）A.400B.500C.100D.1100（3）在△ABC中，∠A=800,∠B=∠C，则∠B=（）A.500B.400C.100D.450二、填空（1）∠A:∠B:∠C=3:4:5，则∠B=（2）∠C=900，∠A=300，则∠B=（3）∠B=800，∠A=3∠C，则∠A=B600750B600A1.三角形的内角和等于1800.△ABC中,∠A+∠B+∠C=1800.小结拓展2、三角形的一个外角等于和它不相邻的两个内角的和。3、三角形最多有一个直角或一个钝角作业布置：教材48页练习第二题、第三题