平面的基本性质第1课时VIP免费

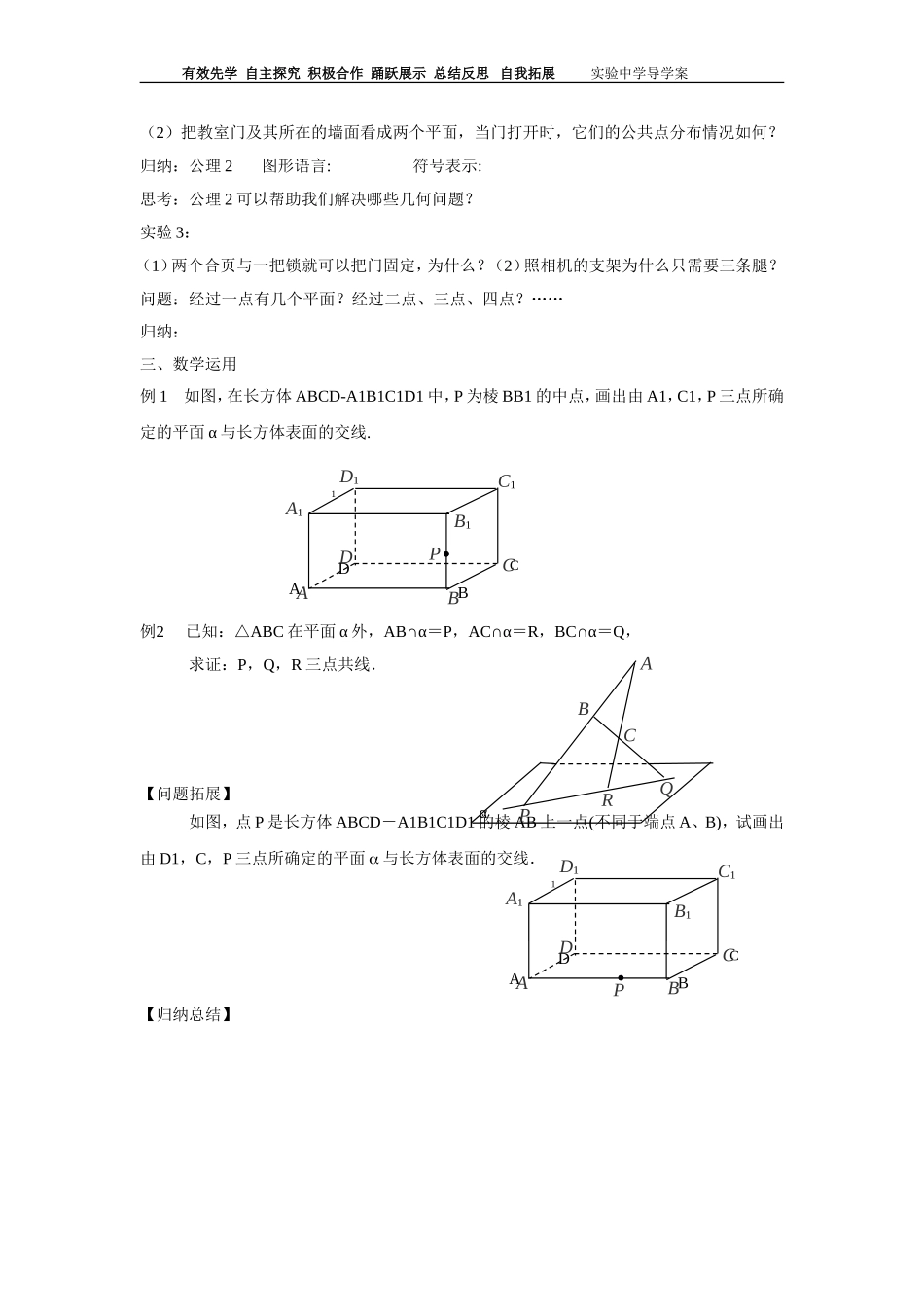
有效先学自主探究积极合作踊跃展示总结反思自我拓展实验中学导学案第1课时平面的基本性质【学习重点】1.初步理解平面的概念；2.了解平面的基本性质（公理1、2、3）；3.能正确使用集合符号表示有关点、线、面的位置关系；4.能运用平面的基本性质解决一些简单的问题．【学习难点】1.对平面的基本性质的理解.2.平面的基本性质的应用.【教材助读】1．平面的概念2．平面的基本性质（公理1、2、3）【预习反馈】：下列叙述中，正确的是_______①因为Pα，Qα，所以PQα；②因为Pα，Q，所以α∩＝PQ；③因为ABα，CAB，DAB，所以CDα；④因为ABα，ABβ，所以∩＝AB.【课堂探究】一、学生活动思考、联想列举出诸如平静的水面、广阔的平原、光滑的桌面、黑板面等等平面的形象．进而归纳出它们的共同特征是平坦的、与厚薄无关．二、建构数学1．平面的认识（无限延展的、没有厚薄）；2．平面的表示；(1)图形语言通常用平行四边形表示平面(2)符号语言通常用希腊字母α、β、γ等来表示，也可以用表示平行四边形的对角顶点字母来表示，如平面α、平面AC等3.点、直线、平面之间的基本关系4．平面的基本性质；实验1：把直尺和桌面分别看作一条直线和一个平面.（1）若直尺的两个端点在桌面内，问直尺所在直线上各点与桌面所在的平面有何关系？（2）若直尺有一个端点不在桌面内，直尺所在的直线与桌面所在的平面的关系如何？得出：公理1图形语言:符号表示:思考：公理1的作用是什么？实验2：（1）把一个三角板的一个角立在桌面上，观察三角板所在的平面与桌面所在的平面有几个公共点.有效先学自主探究积极合作踊跃展示总结反思自我拓展实验中学导学案（2）把教室门及其所在的墙面看成两个平面，当门打开时，它们的公共点分布情况如何？归纳：公理2图形语言:符号表示:思考：公理2可以帮助我们解决哪些几何问题？实验3：（1）两个合页与一把锁就可以把门固定，为什么？（2）照相机的支架为什么只需要三条腿？问题：经过一点有几个平面？经过二点、三点、四点？……归纳：三、数学运用例1如图，在长方体ABCD-A1B1C1D1中，P为棱BB1的中点，画出由A1，C1，P三点所确定的平面α与长方体表面的交线.例2已知：△ABC在平面α外，AB∩α＝P，AC∩α＝R，BC∩α＝Q，求证：P，Q，R三点共线．【问题拓展】如图，点P是长方体ABCD－A1B1C1D1的棱AB上一点(不同于端点A、B)，试画出由D1，C，P三点所确定的平面与长方体表面的交线．【归纳总结】ABCD1A1C1B1D1ABCDPPABCRQαABCD1A1C1B1D1ABCDP