第03讲平面汇交力系VIP免费

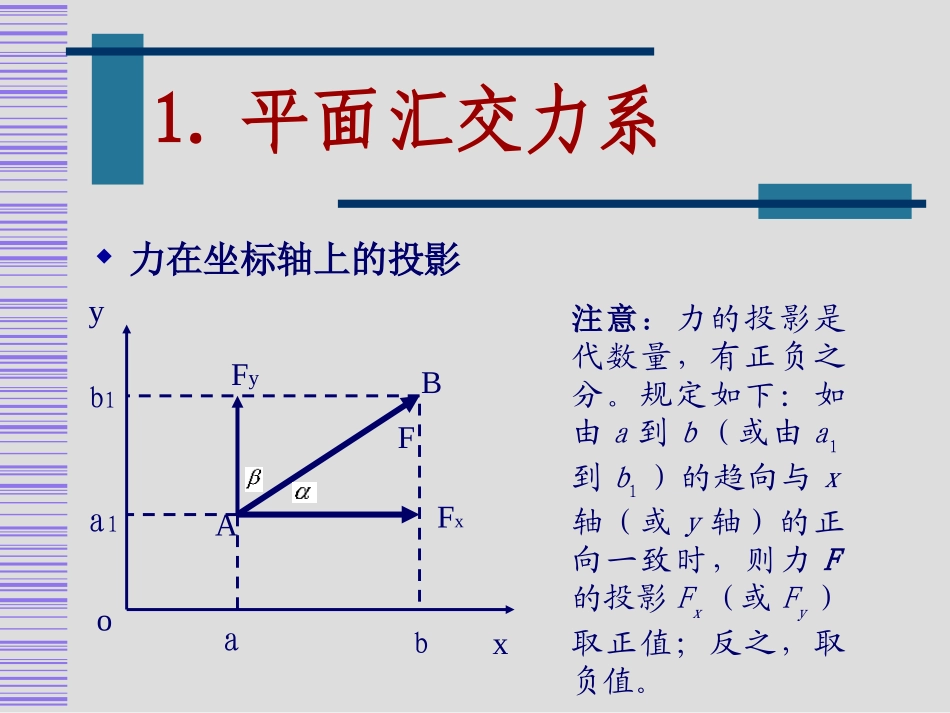
第2章平面力系力系平面力系空间力系汇交力系一般力系汇交力系平行力系平行力系一般力系1.平面汇交力系力的合成与分解力的合成：平行四边形公里F=F1+F2力的分解：公式F=F1+F2中有六个要素，已知其中四个才能确定其余两个。即在已知合力的大小和方向的条件下，还必须给出另外两个条件。工程中常会遇到要将一个力沿已知方向分解，求两分力大小的问题。如求力F在坐标轴上的分力大小。1.平面汇交力系力在坐标轴上的投影注意：力的投影是代数量，有正负之分。规定如下：如由a到b（或由a1到b1）的趋向与x轴（或y轴）的正向一致时，则力F的投影Fx（或Fy）取正值；反之，取负值。AFyoxBaba1b1FxFy1.平面汇交力系若已知力F在直角坐标轴上的投影，则该力的大小和方向为：若已知力F的大小为F，它和x轴的夹角为，则力在坐标轴上的投影可按下式计算：22coscosxyxyFFFFFFFcossinxyFFFF1.平面汇交力系合力投影定理：合力在某一轴上的投影等于各分力在同一轴上投影的代数和。它是用解析法求解平面汇交力系合成与平衡问题的理论依据。ynyyyyxnxxxxFFFFFFFFFF21211.平面汇交力系平面汇交力系的平衡条件：该力系的合力F等于零，即力系中所有力在任选两个坐标轴上投影的代数和均为零。平面汇交力系的平衡方程：00yxFF1.平面汇交力系静力学平衡问题的一般方法和步骤：（1）选择研究对象（2）画受力图（3）建立坐标系，根据平衡条件列平衡方程例1.如图所示吊环受到三条钢丝绳的拉力作用。已知F1=2000N，F2=5000N，F3=3000N。试求合力。解建立如图坐标系。分别计算各力的投影。112000xFFN22cos3050000.8664330xFFNN03xF01yFNNFFy25005.0500030sin22NFFy3000332000433006330xxFFNNNNFFyy55003000250002222633055008386xyFFFNN则合力的大小为：由合力投影定理可得：由于Fx、Fy都是负值，所以合力应在第三象限：cos/6330/83860.7548xFF41例2.如图所示一简易起重机装置，重量G=2kN的重物吊在钢丝绳的一端，钢丝绳的另一端跨过定滑轮A，绕在绞车D的鼓轮上，定滑轮用直杆AB和AC支承，定滑轮半径忽略不计，定滑轮、直杆以及钢丝绳的重量不计，各处接触都为光滑。试求当重物被匀速提升时，杆AB、AC所受的力。FGFABFACxy解:取滑轮为研究对象，作出它的受力图并建立如图直角坐标系。由平面汇交力系平衡条件列平衡方程：FGFABFACxy030cos30sinGFFNAC030sin30cosFFFNACNABcos30220.8667.46sin300.5NACGFFkNkNcos30sin30NABNACFFF7.460.86620.55.46kNkNFNAC为负值，表明FNAC的实际指向与假设方向相反，其反作用力为AC杆所受的力，所以AC杆为受压杆件。2.力矩与平面力偶系力对点之矩概念：力使物体产生转动效应的物理量称为力矩。产生转动的中心点称为力矩中心（简称矩心），力的作用线到力矩中心的距离d称为力臂，力使物体绕矩心转动的效应取决于力F的大小与力臂d的乘积及力矩的转动方向。力对点之矩用MO（F）来表示，即：FdFMO力矩是代数量，式中的正负号用来表明力矩的转动方向。规定力使物体绕矩心作逆时针方向转动时，力矩取正号；反之，取负号。力矩的单位是或mkNmN2.力矩与平面力偶系合力矩定理：平面汇交力系的合力对平面内任意一点之矩，等于其所有分力对同一点的力矩的代数和。即：1nOOiiMFMF2.力矩与平面力偶系力对点之矩的求法方法1：用力矩的定义式，即力和力臂的乘积求力矩。这种方法的关键在于确定力臂d。需要注意的是，力臂d是矩心到力作用线的距离，即力臂必须垂直于力的作用线。方法2：运用合力矩定理求力矩。在工程实际中，有时力臂的几何关系较复杂，不易确定时，可将作用力正交分解为两个分力，然后应用合力矩定理求原力对矩心的力矩。例：如图所示，构件OBC的O端为铰链支座约束，力F作用于C点，其方向角为，又知OB=，BC=，...