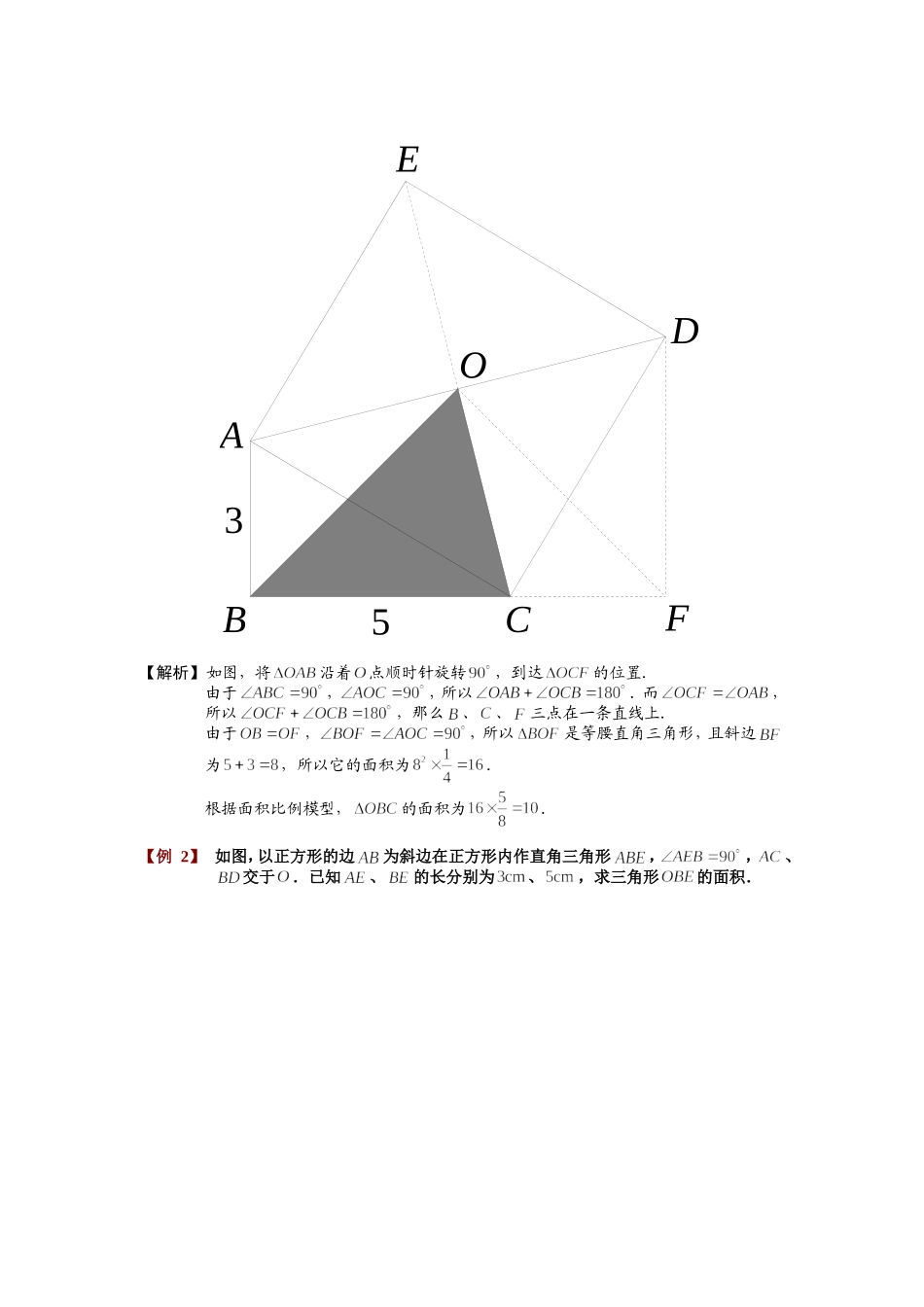
培优提升------平面几何部分5【例1】如图所示,中,,,,以为一边向外作正方形,中心为,求的面积.53OABCDEF53OABCDE【解析】如图,将沿着点顺时针旋转,到达的位置.由于,,所以.而,所以,那么、、三点在一条直线上.由于,,所以是等腰直角三角形,且斜边为,所以它的面积为.根据面积比例模型,的面积为.【例2】如图,以正方形的边为斜边在正方形内作直角三角形,,、交于.已知、的长分别为、,求三角形的面积.ABCDOEFABCDOE【解析】如图,连接,以点为中心,将顺时针旋转到的位置.那么,而也是,所以四边形是直角梯形,且,所以梯形的面积为:().又因为是直角三角形,根据勾股定理,,所以().那么(),所以().【例3】如下图,六边形中,,,,且有平行于,平行于,平行于,对角线垂直于,已知厘米,厘米,请问六边形ABCDEF的面积是多少平方厘米?FEABDCGFEABDC【解析】如图,我们将BCD平移使得CD与AF重合,将DEF平移使得ED与AB重合,这样EF、BC都重合到图中的AG了.这样就组成了一个长方形BGFD,它的面积与原六边形的面积相等,显然长方形BGFD的面积为2418432平方厘米,所以六边形ABCDEF的面积为432平方厘米.【例4】如图,三角形ABC的面积是1,E是AC的中点,点D在BC上,且:1:2BDDC,AD与BE交于点F.则四边形DFEC的面积等于.FEDCBA33321FEDCBAABCDEFFEDCBA【解析】方法一:连接CF,根据燕尾定理,12ABFACFSBDSDC△△,1ABFCBFSAESEC△△,设1BDFS△份,则2DCFS△份,3ABFS△份,3AEFEFCSS△△份,如图所标所以551212DCEFABCSS△方法二:连接DE,由题目条件可得到1133ABDABCSS△△,11212233ADEADCABCSSS△△△,所以11ABDADESBFFES△△,111111122323212DEFDEBBECABCSSSS△△△△,而211323CDEABCSS△△.所以则四边形DFEC的面积等于512.【巩固】如图,长方形ABCD的面积是2平方厘米,2ECDE,F是DG的中点.阴影部分的面积是多少平方厘米?xyyxABCDEFGGFEDCBA33GFEDCBA213【解析】设1DEFS△份,则根据燕尾定理其他面积如图所示551212BCDSS△阴影平方厘米.【例5】四边形ABCD的对角线AC与BD交于点O(如图所示).如果三角形ABD的面积等于三角形BCD的面积的13,且2AO,3DO,那么CO的长度是DO的长度的_________倍.ABCDOHGABCDO【解析】在本题中,四边形ABCD为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形.看到题目中给出条件:1:3ABDBCDSS,这可以向模型一蝴蝶定理靠拢,于是得出一种解法.又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH垂直BD于H,CG垂直BD于G,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之比,得出结果.请老师注意比较两种解法,使学生体会到蝴蝶定理的优势,从而主观上愿意掌握并使用蝴蝶定理解决问题.解法一:∵::1:3ABDBDCAOOCSS,∴236OC,∴:6:32:1OCOD.解法二:作AHBD于H,CGBD于G.∵13ABDBCDSS,∴13AHCG,∴13AODDOCSS,∴13AOCO,∴236OC,∴:6:32:1OCOD.【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AGGC?ABCDG321【解析】⑴根据蝴蝶定理,123BGCS,那么6BGCS;⑵根据蝴蝶定理,:12:361:3AGGC.