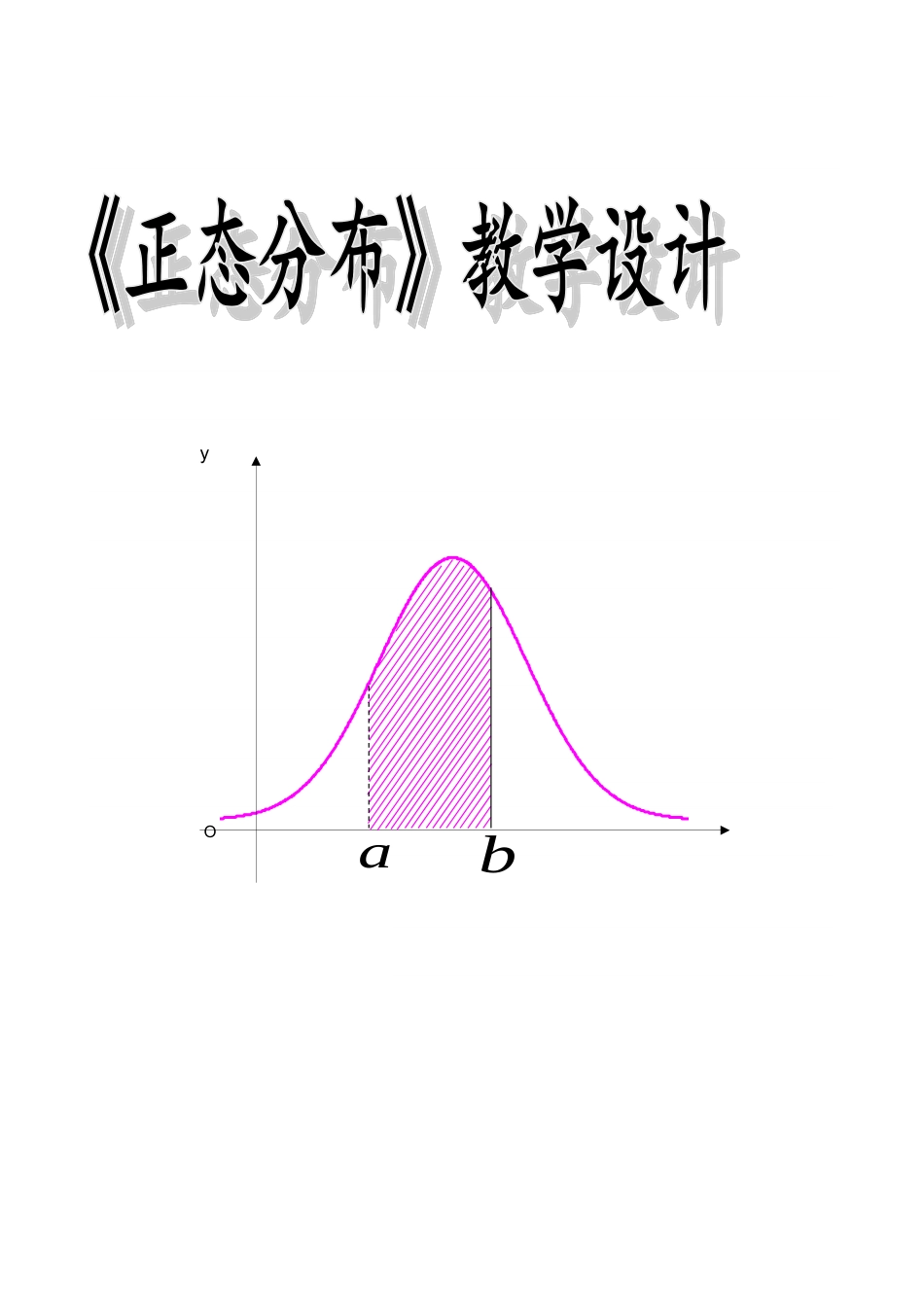
Oyab正态分布【教学内容】正态分布是高中数学人教A版选修2-3教材第二章的重要内容。本节主要了解一种最常见的、有着广泛应用的分布——正态分布,直观认识正态曲线的形状、特点,正态曲线所表示的意义,正态分布的两个重要参数,对正态曲线位置和形状的影响。【教学目标】1、知识与技能结合正态曲线,加深对正态密度函数的理解;通过正态分布的图形特征,归纳正态曲线的性质.2、过程与方法讲授法与引导发现法.通过教师先讲,师生再共同探究的方式,让学生深刻理解相关概念,领会数形结合的数学思想方法,体会数学知识的形成.3、情感态度与价值观通过教学中一系列的探究过程使学生体验发现的快乐,形成积极的情感,培养学生的进取意识和科学精神.【学情分析】通过前面知识的学习,学生已经掌握了平均数、标准差、频率分布直方图、折线图等研究数据的知识与方法,为学习正态分布这一生活中常见的连续性随机变量所服从的分布打下了良好的基础;此外,学生在生活中也有了不少的常识积累,为正态分布的学习提供了便利;但由于学生所学知识范围的限制,对正态分布函数的来龙去脉不可能深究。【教学重点与难点】重点:正态分布曲线的特点及其所表示的意义;难点:了解在实际中什么样的随机变量服从正态分布,并掌握正态分布曲线所表示的意义.【教学方法】实验探究、学案导学、多媒体辅助【教具准备】黑板,多媒体,高尔顿试验板【教学过程设计】教学环节教学内容师生互动设计意图创设情境1.全国划骑跑铁人三项挑战赛成绩分布;2.学生上台演示高尔顿板试验.创设情境,为导入新知做准备.学生感悟体验,对试验的结果进行定向思考.[来源:Zxxk.Com]学生经过观察小球在槽中的堆积形状发现:下落的小球在槽中的分布是有规律的.让学生演示试验,能提高学生的学习积极性,提高学习数学的兴趣.让学生体验“正态分布曲线“的生成和发现历程.建构概念1.用频率分布直方图从频率角度研究小球的分布规律.⑴将球槽编号,算出各个球槽内的小球个数,作出频率分布表.⑵以球槽的编号为横坐标,以小球落入各个球槽内的频率与组距的比值为纵坐标,画出频率分布直方图。连接各个长方形上端的中点得到频率分布折线图.[来源:Zxxk.Com]引导学生思考回顾,教师通过课件演示作图过程.在这里引导学生回忆得到,此处的纵坐标为频率除以组距.教师提出问题:这里每个长方形的面积的含义是什么?学生经过回忆,易得:长方形面积代表相应区间内数据的频率.通过把与新内容有关的旧知识抽出来作为新知识的“生长点”,为引入新知搭桥铺路,形成正迁移.通过这里的思考回忆,加深对频率分布直方图的理解.建构概(3)随着试验次数增多,折线图就越来越接近于一条光滑的曲线.分析表达式特点:解析式中前有一个系数,后面是一个以为底数的指数形式,幂指数为,解析式中含两个常数和,还含有两个参数和,分别指总体随机变量的平均数和标准差,可用样本平均与旧教材不同的是,该处在学生从形的角度直观认识了正态曲线之后才给出曲线对应的表达式,这样处理能更直观,学生更易理解正态曲线的来源.课后作业念从描述曲线形状的角度自然引入了正态密度函数的表达式:数和标准差去估计.列举实例请学生结合高尔顿板试验讨论提出的问题,并尝试归纳服从或近似服从正态分布的随机变量所具有的特征:1.小球落下的位置是随机的吗?2.若没有上部的小木块,小球会落在哪里?是什么影响了小球落下的位置?3.前一个小球对下一个小球落下的位置有影响吗?哪个小球对结果的影响大?4.你能事先确定某个小球下落时会与哪些小木块发生碰撞吗?学生通过讨论,教师引导学生得出问题的结果:1.它是随机的.2.竖直落下.受众多次碰撞的影响.3.互不相干、不分主次.4.不能,具有偶然性.然后归纳出特征:一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用之和,它就服从或近似服从正态分布.教师列举实例分析,帮助学生更加透彻的理解.“什么样的随机变量服从(或近似服从)正态分布?”是本节课的难点,采用设置问题串的方式,将复杂的问题分解成几个容易解决的问题,能有效突破难点.同时采用小组讨论的形式...