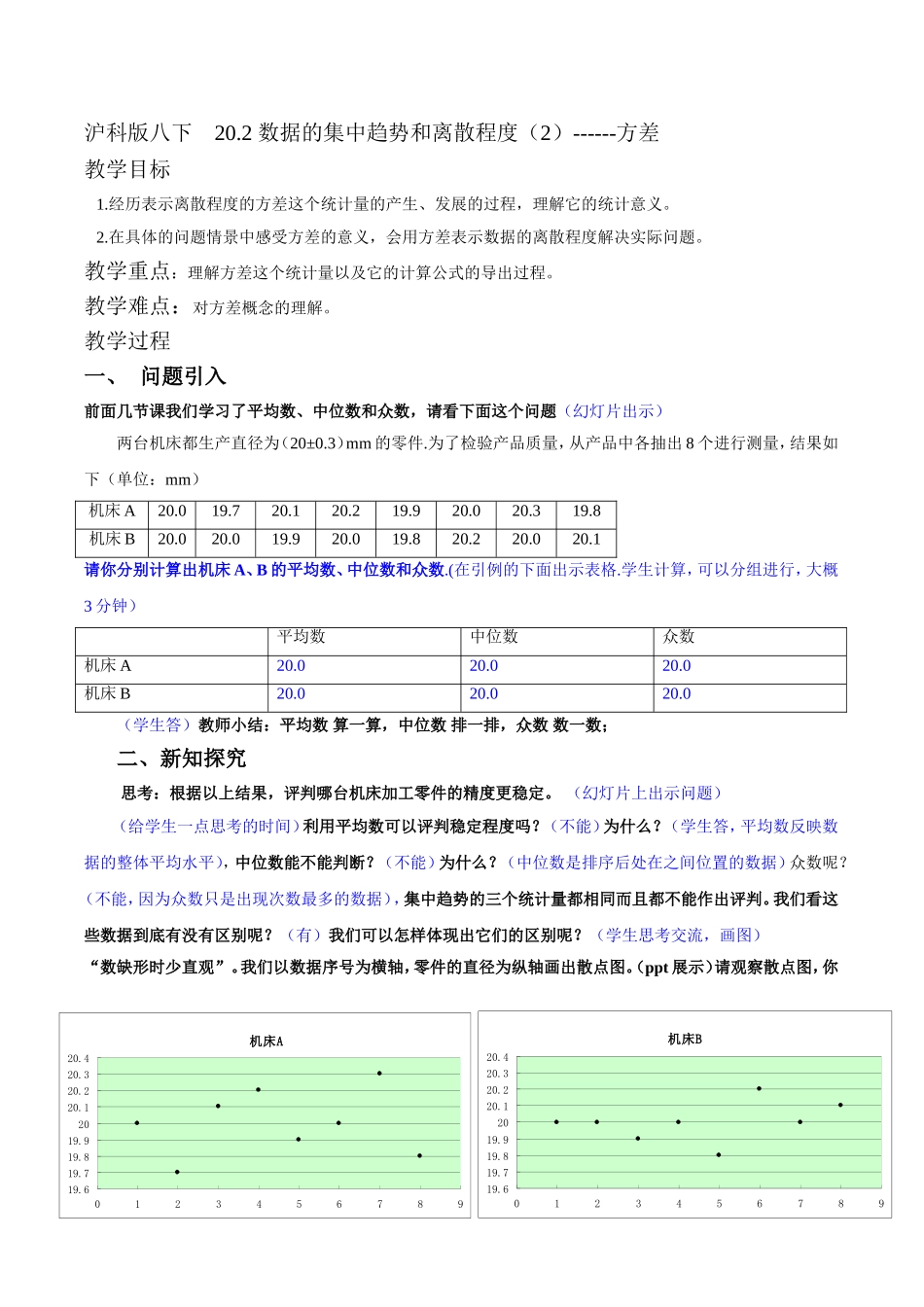
沪科版八下20.2数据的集中趋势和离散程度(2)------方差教学目标1.经历表示离散程度的方差这个统计量的产生、发展的过程,理解它的统计意义。2.在具体的问题情景中感受方差的意义,会用方差表示数据的离散程度解决实际问题。教学重点:理解方差这个统计量以及它的计算公式的导出过程。教学难点:对方差概念的理解。教学过程一、问题引入前面几节课我们学习了平均数、中位数和众数,请看下面这个问题(幻灯片出示)两台机床都生产直径为(20±0.3)mm的零件.为了检验产品质量,从产品中各抽出8个进行测量,结果如下(单位:mm)机床A20.019.720.120.219.920.020.319.8机床B20.020.019.920.019.820.220.020.1请你分别计算出机床A、B的平均数、中位数和众数.(在引例的下面出示表格.学生计算,可以分组进行,大概3分钟)平均数中位数众数机床A20.020.020.0机床B20.020.020.0(学生答)教师小结:平均数算一算,中位数排一排,众数数一数;二、新知探究思考:根据以上结果,评判哪台机床加工零件的精度更稳定。(幻灯片上出示问题)(给学生一点思考的时间)利用平均数可以评判稳定程度吗?(不能)为什么?(学生答,平均数反映数据的整体平均水平),中位数能不能判断?(不能)为什么?(中位数是排序后处在之间位置的数据)众数呢?(不能,因为众数只是出现次数最多的数据),集中趋势的三个统计量都相同而且都不能作出评判。我们看这些数据到底有没有区别呢?(有)我们可以怎样体现出它们的区别呢?(学生思考交流,画图)“数缺形时少直观”。我们以数据序号为横轴,零件的直径为纵轴画出散点图。(ppt展示)请观察散点图,你机床B19.619.719.819.92020.120.220.320.40123456789机床A19.619.719.819.92020.120.220.320.40123456789能评判哪台机床加工零件的精度更稳定吗?(略停顿,同桌交流。学生答:机床B)你怎么看出来的?(直观上数据A较分散,数据B较集中,或者说波动程度明显区别)带着学生分析散点图,分散、集中是相比较而言的,和谁作比较?(20.0)20.0是生产的标准同时也是平均数(ppt上使用动画把20这条直线用红色加粗的线体现出来,动画闪烁两次)处理类似的问题,画图一般很麻烦,而且如果直观感知不明显怎么办呢?我们考虑能不能用某个数量来反映呢?集中趋势的三个统计量都不行,我们今天就从另一个角度观察数据(板书:20.2数据的离散程度)刚才我们分析数据的波动是与平均数比较。我们先把每个数据与平均数的偏离程度算出来,怎么算?(生答:每个数据-平均数)我们把这个差叫偏差。(以A为例,教师板演)(板书:机床A)大家把机床B的数据求偏差。(学生计算)如何整体的处理这些差,你有什么想法?(求和)动手算一算(两组数据都是0)求和时出现了正负抵消的情况,偏离平均数的程度没有区别出来。怎么样可以避免求和时的正负抵消呢,你有什么方法?(学生思考交流,学生答:平方,学生答什么马上抓生成,师生合作算一算,偏差的平方和不是零了。还有没有别的避免正负抵消的方法?(绝对值也可以)是的,绝对值的几何意义就是距离,但是为了方便计算,统计学中选择了平方运算,事实上,平方运算会使得偏差大的更大,小的更小,这样差别更加明显,便于分析。大家觉得呢?同学们,如果两组数据总数不相同,只求偏差平方和的话就不一定公平了,(稍停顿)怎么解决呢?(学生答,计算平均数)你怎么想到的?(学生答,平均水平)很好,求平均数不仅能解决个数不同时的状况。而且求平均数就是求落实到每个数据上的偏差是多少。(学生把B的运算在学案上完成)这个量在统计学中叫做方差。回顾一下,方差是怎样的运算过程?(特殊到一般,抽象出公式)(板书课题:方差的定义:一般的,一组数据为,平均数为,那么称为方差,(追问:方差有什么作用?)刻画数据的离散程度。方差的单位和原单位什么关系呢?(学生答)所以,机床A的方差是0.035(mm2),它们的方差不同,你知道要怎么评判哪台机床加工零件的精度更稳定吗?(学生答),“形缺数时难入微”,数形结合,通过散点图分析得出方差越小数据越稳定。教师板书。)引例的思考得以解决。方差这个统计量刻画数...