相似三角形相似的判定（第2课时）VIP免费

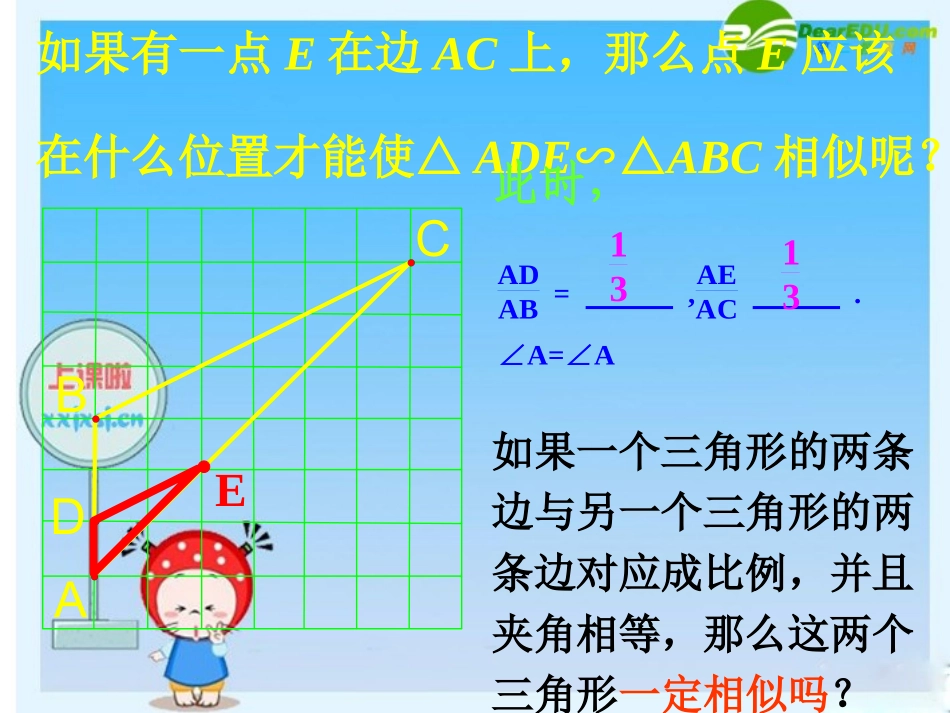
24.3.2相似三角形的判定（第2课时）24.3.2相似三角形的判定（第2课时）判断两个三角形相似,你有哪些方法方法1：通过定义（不常用）方法2：通过平行线。方法3：两角对应相等，两三角形相似即三角对应相等，三边对应成比例的两三角形相似DCBA如果有一点E在边AC上，那么点E应该在什么位置才能使△ADE∽△ABC相似呢？此时，如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形一定相似吗？EADAB=,AEAC.∠A=∠A13131、如图，在△ABC和△A′B′C′中，∠A＝∠A′，,比较∠B和∠B′的大小.由此，你能判断△ABC和△A′B′C′相似吗？为什么？2CAACBAABABCA′B′C′KCAACBAAB2、在上题的条件下，设改变k的值的大小，（∠A＝∠A′不变）再试一试，你能判断△ABC与△A′B′C′相似吗？ABCA′B′C′B″C″'C'AAC'B'AABCAACBAAB''''CAACBAAB如图，在△ABC和△A′B′C′中，∠A＝∠A′，，那么△ABC∽△A′B′C′解：假设AB＞A′B′，在AB上截取AB″＝A′B′，过点B″作B″C″∥BC，交AC于点C″，在△ABC和△AB″C″，∵B″C″∥BC∴△ABC∽△AB″C″，∴又∵AB″＝A′B′，∴AC″＝A′C′，∵∠A＝∠A′，∴△AB″C″≌△A′B′C′，∴△ABC∽△A′B′C′ABCA′B′C′B″C″由此得判定方法二：如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似。几何语言：∵在△ABC和△A′B′C′中，∠A＝∠A′，'C'AAC'B'AAB∴△ABC∽△A′B′C′ABCA′B′C′1、如图，在△ABC和△A′B′C′中，∠B＝∠B′，要使△ABC∽△A′B′C′，还需要添加什么条件？ABCA′B′C′讨论：判定三角形相似的方法之二•两边对应成比例且夹角相等的两个三角形相似.如图,在△ABC与△A′B′C′中,如果那么△ABCA∽△′B′C′(两边对应成比例且夹角相等的两个三角形相似.)CBAA′B′C′.CAACBAAB这又是一个用来判定两个三角形相似的方法,但使用频率不是很高,务必引起重视.且∠A=A∠′,几何语言例1、判断图中△AEB和△FEC是否相似？解：54303645EAFCB12∵AEFE=5436=1.5BECE=4530=1.5∴AEFE=BECE∵∠1=∠2∴△AEB∽△FEC1、下列条件能判定△ABC与△A′B′C′相似的有（）（1）∠A＝45°，AB＝12，AC＝15，∠A′＝45°，A′B′＝16，A′C′＝20（2）∠A＝47°，AB＝1.5，AC＝2，∠B′＝47°，A′B′＝2.8，B′C′＝2.1（3）∠A＝47°，AB＝2，AC＝3，∠B′＝47°，A′B′＝4，B′C′＝6A、0个B、1个C、2个D、3个2、如图，在△ABC中，AB=4cm，AC=2cm。（1）在AB上取一点D，当AD=_____cm时，△ACD∽△ABC；（2）在AC的延长线上取一点E，当CE=____cm时，△AEB∽△ABC；课堂练习CBADE此时，BE与DC有怎样的位置关系？为什么？3、（2012•海南）如图，点D在△ABC的边AC上，要判定△ADB与△ABC相似，添加一个条件，不正确的是（）A．∠ABD=∠CB．∠ADB=∠ABCC.D.ABCBBDCDADABABAC4、如图,在△ABC中,D在AB上,要说明△ACD∽△ABC相似,已经具备了条件,还需添加的条件是，或或.ACDB23ECAEBDADBCDE5、如图，已知,试求的值.ADECB6.△在ABC中，AB>AC，过AB上一点D作直线DE交另一边于E，使所得三角形与原三角形相似，画出满足条件的图形.EDABCDABCDABCDABCEEE知识象一艘船让它载着我们驶向理想的……你今天努力了吗？你今天努力了吗？