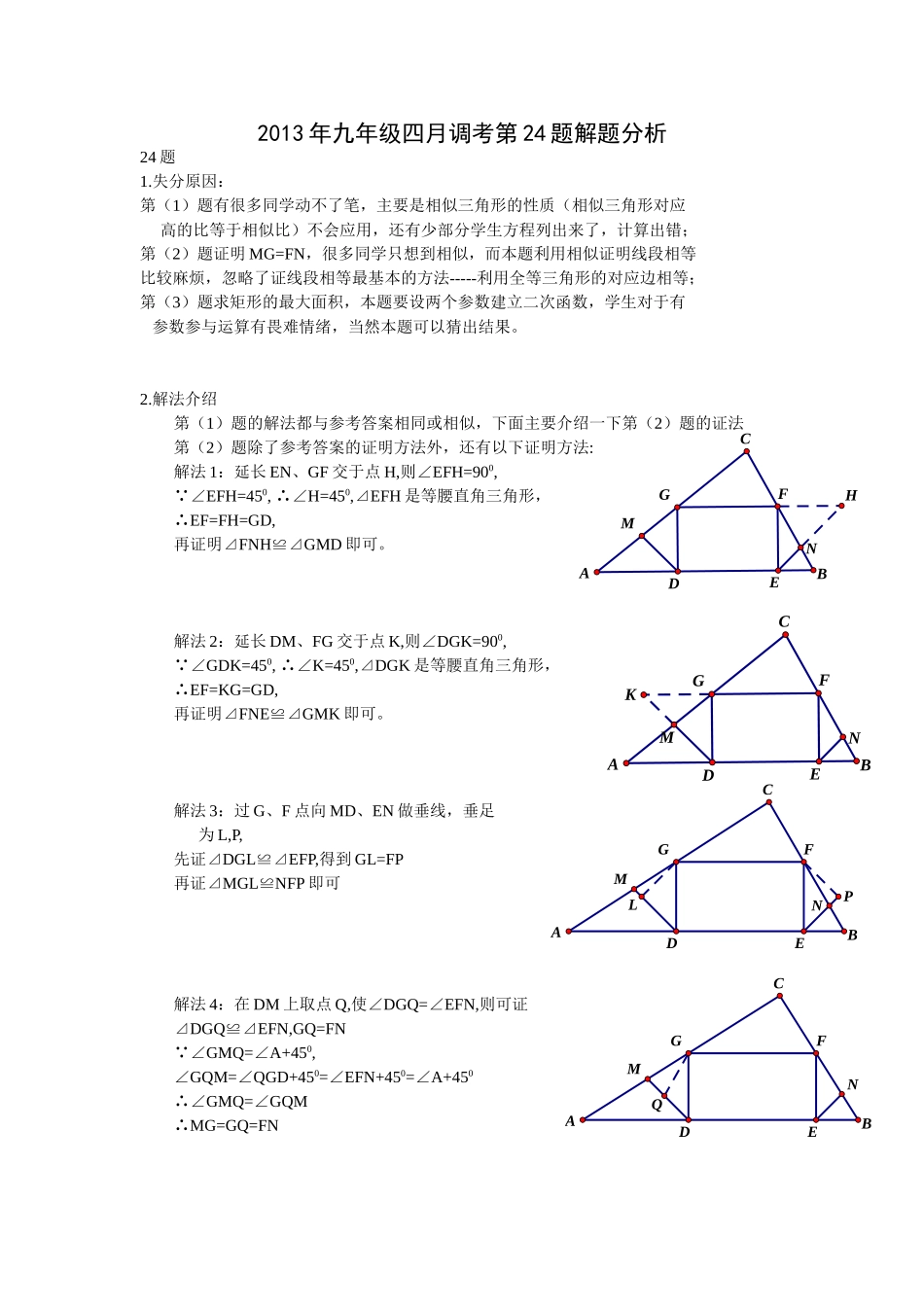
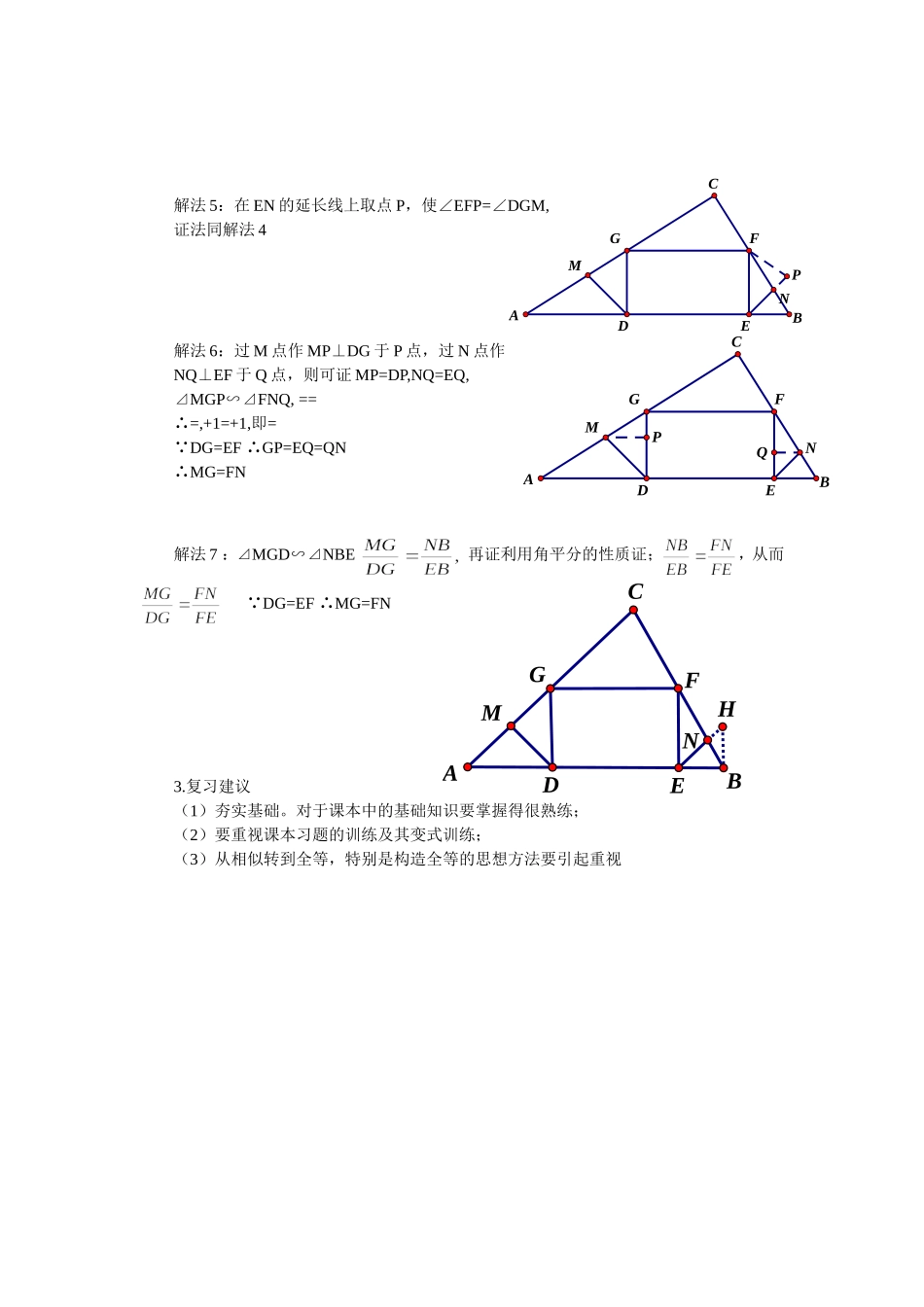
2013年九年级四月调考第24题解题分析24题1.失分原因:第(1)题有很多同学动不了笔,主要是相似三角形的性质(相似三角形对应高的比等于相似比)不会应用,还有少部分学生方程列出来了,计算出错;第(2)题证明MG=FN,很多同学只想到相似,而本题利用相似证明线段相等比较麻烦,忽略了证线段相等最基本的方法-----利用全等三角形的对应边相等;第(3)题求矩形的最大面积,本题要设两个参数建立二次函数,学生对于有参数参与运算有畏难情绪,当然本题可以猜出结果。2.解法介绍第(1)题的解法都与参考答案相同或相似,下面主要介绍一下第(2)题的证法第(2)题除了参考答案的证明方法外,还有以下证明方法:解法1:延长EN、GF交于点H,则∠EFH=900,∵∠EFH=450,∴∠H=450,⊿EFH是等腰直角三角形,∴EF=FH=GD,再证明⊿FNH≌⊿GMD即可。解法2:延长DM、FG交于点K,则∠DGK=900,∵∠GDK=450,∴∠K=450,⊿DGK是等腰直角三角形,∴EF=KG=GD,再证明⊿FNE≌⊿GMK即可。解法3:过G、F点向MD、EN做垂线,垂足为L,P,先证⊿DGL≌⊿EFP,得到GL=FP再证⊿MGL≌NFP即可解法4:在DM上取点Q,使∠DGQ=∠EFN,则可证⊿DGQ≌⊿EFN,GQ=FN∵∠GMQ=∠A+450,∠GQM=∠QGD+450=∠EFN+450=∠A+450∴∠GMQ=∠GQM∴MG=GQ=FNHNMEDFCABGKNMEDFCABGPLNMEDFCABGNMEDFCABGQABCHGFEDMN解法5:在EN的延长线上取点P,使∠EFP=∠DGM,证法同解法4解法6:过M点作MP⊥DG于P点,过N点作NQ⊥EF于Q点,则可证MP=DP,NQ=EQ,⊿MGP∽⊿FNQ,==∴=,+1=+1,即=∵DG=EF∴GP=EQ=QN∴MG=FN解法7:⊿MGD∽⊿NBE再证利用角平分的性质证;,从而∵DG=EF∴MG=FN3.复习建议(1)夯实基础。对于课本中的基础知识要掌握得很熟练;(2)要重视课本习题的训练及其变式训练;(3)从相似转到全等,特别是构造全等的思想方法要引起重视NMEDFCABGPQPNMEDFCABG