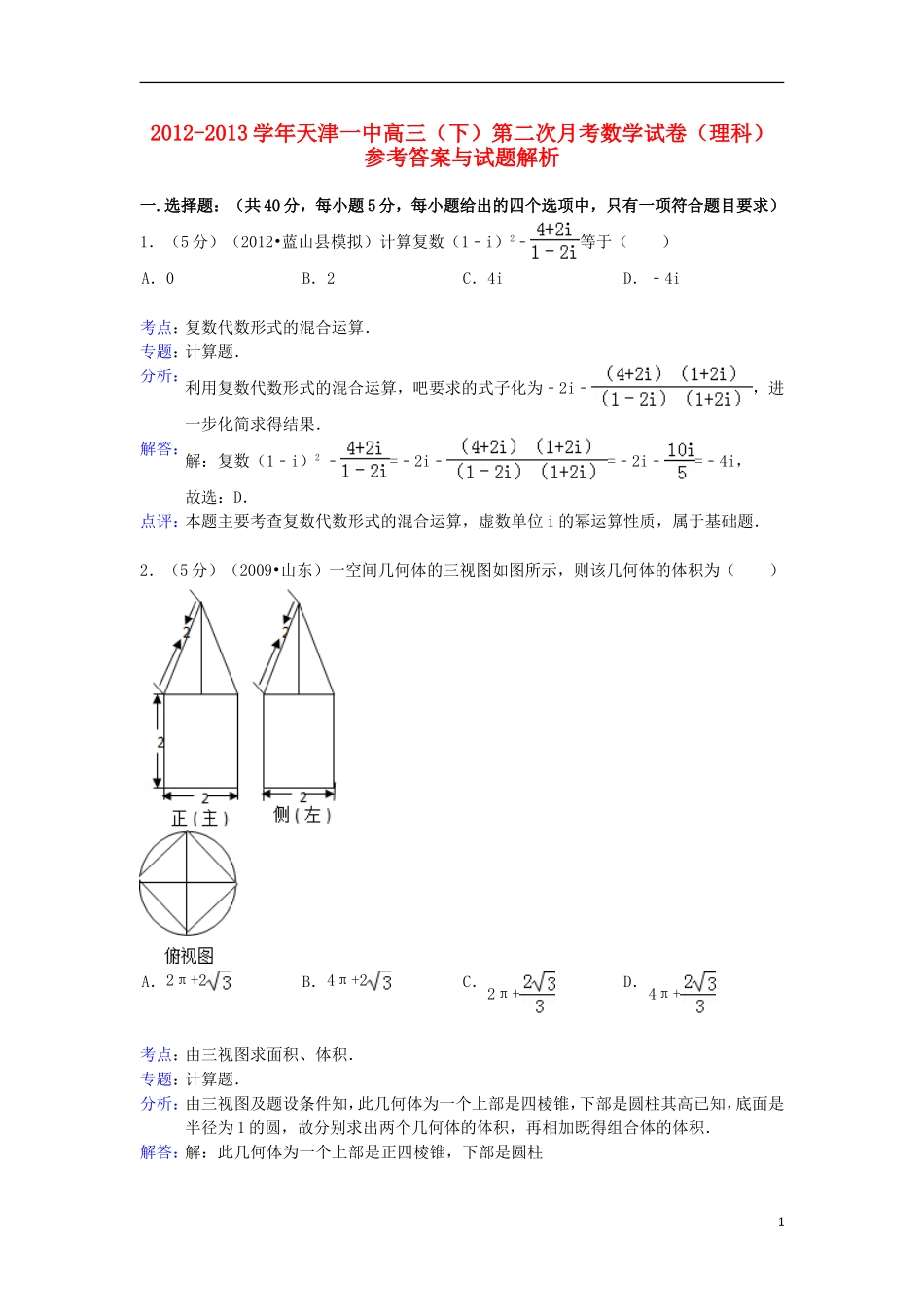
2012-2013学年天津一中高三(下)第二次月考数学试卷(理科)参考答案与试题解析一.选择题:(共40分,每小题5分,每小题给出的四个选项中,只有一项符合题目要求)1.(5分)(2012•蓝山县模拟)计算复数(1﹣i)2﹣等于()A.0B.2C.4iD.﹣4i考点:复数代数形式的混合运算.专题:计算题.分析:利用复数代数形式的混合运算,吧要求的式子化为﹣2i﹣,进一步化简求得结果.解答:解:复数(1﹣i)2﹣=﹣2i﹣=﹣2i﹣=﹣4i,故选:D.点评:本题主要考查复数代数形式的混合运算,虚数单位i的幂运算性质,属于基础题.2.(5分)(2009•山东)一空间几何体的三视图如图所示,则该几何体的体积为()A.2π+2B.4π+2C.2π+D.4π+考点:由三视图求面积、体积.专题:计算题.分析:由三视图及题设条件知,此几何体为一个上部是四棱锥,下部是圆柱其高已知,底面是半径为1的圆,故分别求出两个几何体的体积,再相加既得组合体的体积.解答:解:此几何体为一个上部是正四棱锥,下部是圆柱1由于圆柱的底面半径为1,其高为2,故其体积为π×12×2=2π棱锥底面是对角线为2的正方形,故其边长为,其底面积为2,又母线长为2,故其高为由此知其体积为=故组合体的体积为2π+故选C点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是组合体的体积,其方法是分部来求,再求总体积.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”.三视图是高考的新增考点,不时出现在高考试题中,应予以重视.3.(5分)极坐标方程ρ=cosθ和参数方程(t为参数)所表示的图形分别是()A.圆、直线B.直线、圆C.圆、圆D.直线、直线考点:直线的参数方程;简单曲线的极坐标方程.专题:计算题.分析:极坐标方程ρ=cosθ化为直角坐标方程为,表示一个圆,参数方程(t为参数),消去参数t可得3x+y+1=0,表示一条直线,由此得出结论.解答:解:极坐标方程ρ=cosθ即ρ2=ρcosθ,化为直角坐标方程为x2+y2=x,即,表示一个圆.参数方程(t为参数),消去参数t可得3x+y+1=0,表示一条直线,故选A.点评:本题主要考查把极坐标方程化为直角坐标方程的方法,把参数方程化为普通方程的方法,直线的方程特征、圆的标准方程,属于基础题.4.(5分)若△ABC的三个内角成等差数列,三边成等比数列,则△ABC是()A.直角三角形B.等腰直角三角形C.等边三角形D.钝角三角形考点:三角形的形状判断.2专题:计算题;解三角形.分析:先确定三角形必有一内角为60°,再根据对应三边成等比数列,结合余弦定理,即可求得结论.解答:解:由题意不妨设A,B,C成等差数列则2B=A+C A+B+C=π∴B=,A+C= a,b,c成等比数列∴b2=ac, b2=a2+c2﹣2accos60°=a2+c2﹣ac∴a2+c2﹣ac=ac∴(a﹣c)2=0∴a=c B=60°,∴三角形为等边三角形,故选C.点评:本题考查等差数列与等比数列,考查余弦定理,考查学生的计算能力,属于中档题.5.(5分)(2011•汕头一模)在△ABC中,tanA是以﹣4为第3项,4为第7项的等差数列的公差;tanB是以为第3项,9为第6项的等比数列的公比,则该三角形为()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形考点:等比数列的通项公式;两角和与差的正切函数.专题:计算题.分析:首先,由等差数列的通项公式和等比数列的通项公式,结合已知可得tanA=2,tanB=3,然后利用两角和的正切公式可求出tan(A+B)=﹣1,从而求出∠C,再结合题意确定A、B的范围,从而确定△ABC的形状.解答:解:由题意可得,tanA==2,tanB==3,故tan(A+B)==﹣1, 0<A+B<π,∴A+B=,∴∠C=;又 tanA>0,tanB>0,0<A<π,0<B<π,∴0<A<,0<B<,3故△ABC为锐角三角形.故选A.点评:本题通过解三角形问题,考查了等差数列和等比数列的通项公式,两角和的正切公式,综合性较强,难度中等.6.(5分)α,β为平面,m为直线,如果α∥β,那么“m∥α”是“m⊆β”的()A.充分非必要条件B.必要非充分条件C.充要条...