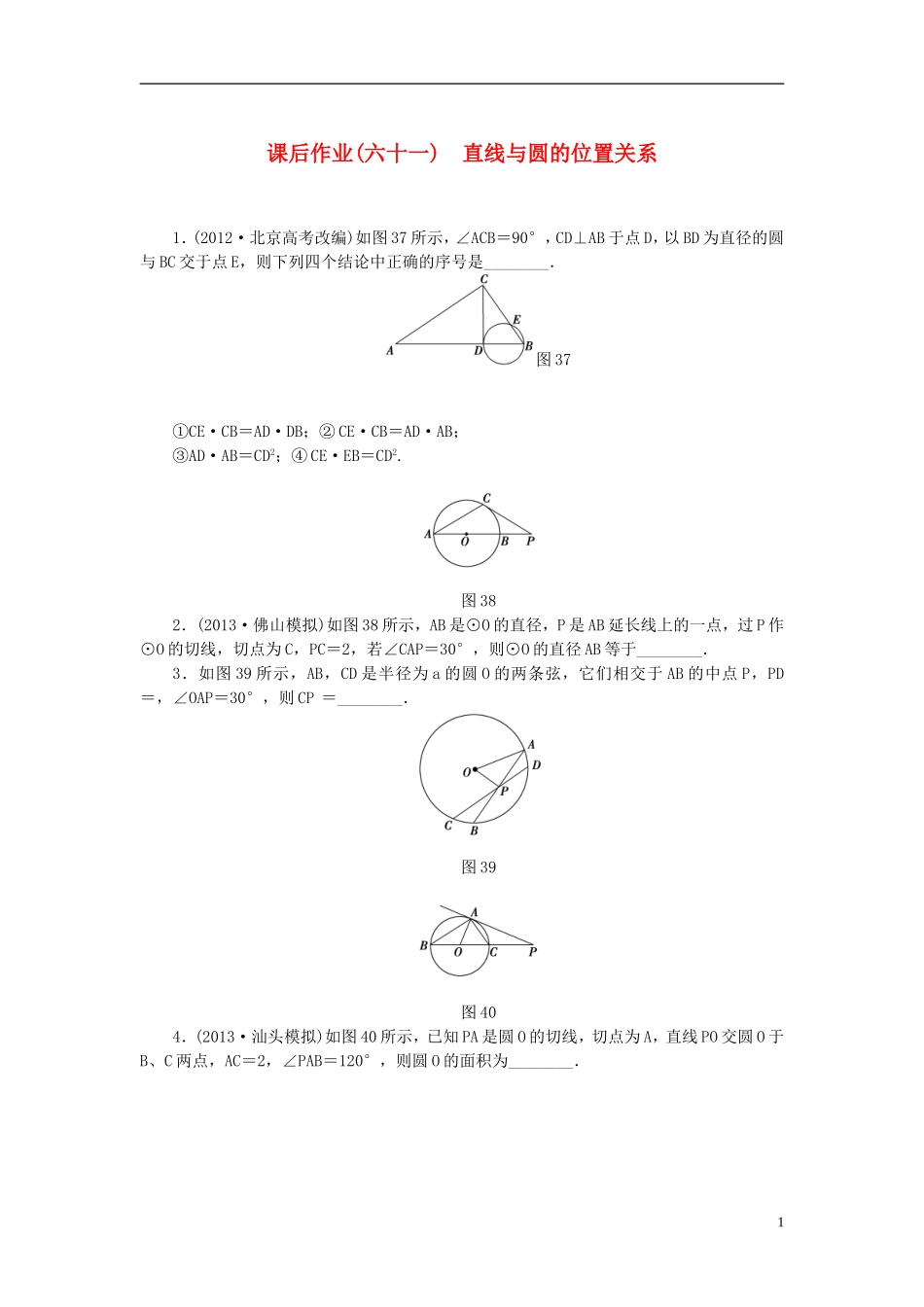
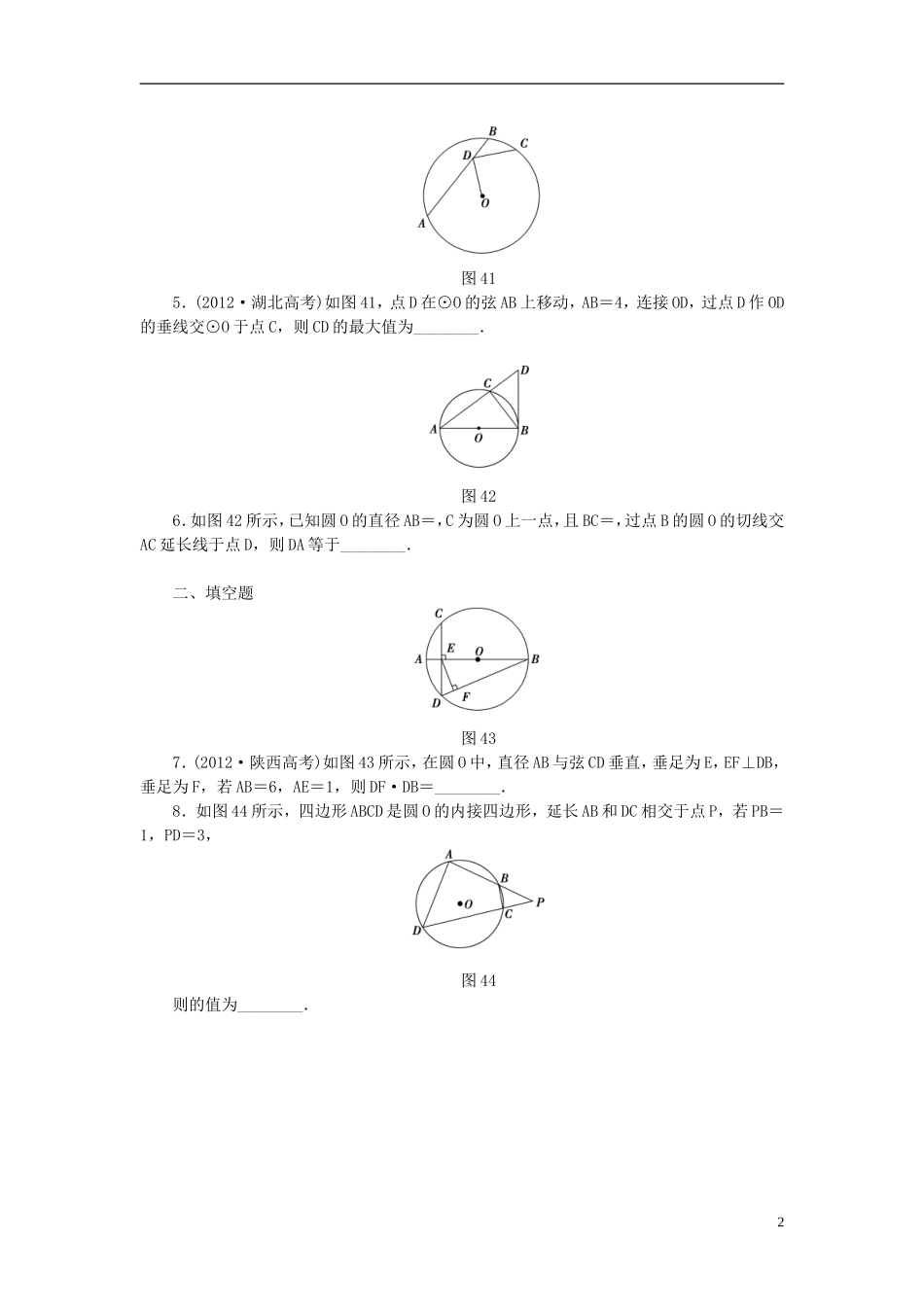
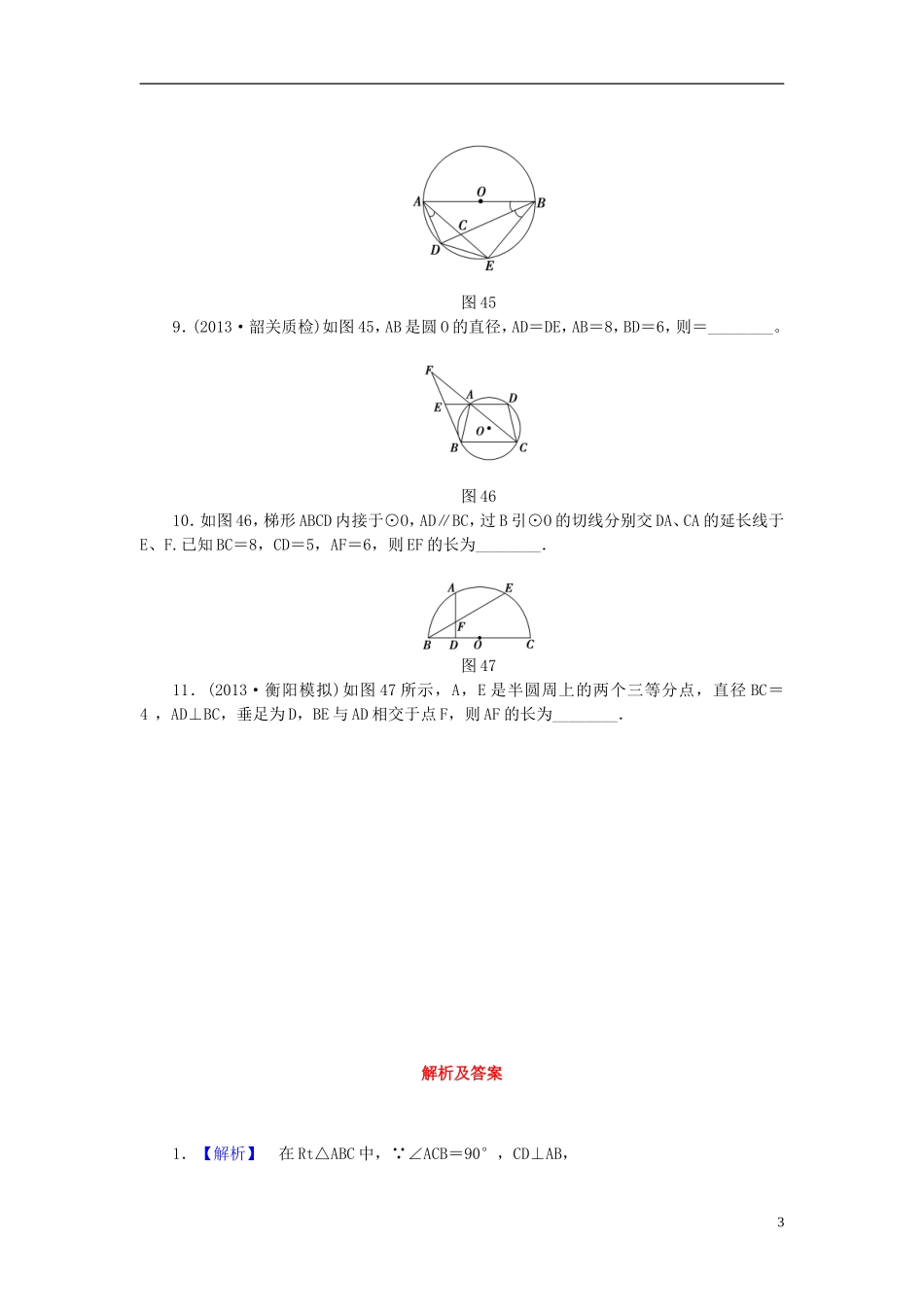
课后作业(六十一)直线与圆的位置关系1.(2012·北京高考改编)如图37所示,∠ACB=90°,CD⊥AB于点D,以BD为直径的圆与BC交于点E,则下列四个结论中正确的序号是________.图37①CE·CB=AD·DB;②CE·CB=AD·AB;③AD·AB=CD2;④CE·EB=CD2.图382.(2013·佛山模拟)如图38所示,AB是⊙O的直径,P是AB延长线上的一点,过P作⊙O的切线,切点为C,PC=2,若∠CAP=30°,则⊙O的直径AB等于________.3.如图39所示,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD=,∠OAP=30°,则CP=________.图39图404.(2013·汕头模拟)如图40所示,已知PA是圆O的切线,切点为A,直线PO交圆O于B、C两点,AC=2,∠PAB=120°,则圆O的面积为________.1图415.(2012·湖北高考)如图41,点D在⊙O的弦AB上移动,AB=4,连接OD,过点D作OD的垂线交⊙O于点C,则CD的最大值为________.图426.如图42所示,已知圆O的直径AB=,C为圆O上一点,且BC=,过点B的圆O的切线交AC延长线于点D,则DA等于________.二、填空题图437.(2012·陕西高考)如图43所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,则DF·DB=________.8.如图44所示,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P,若PB=1,PD=3,图44则的值为________.2图459.(2013·韶关质检)如图45,AB是圆O的直径,AD=DE,AB=8,BD=6,则=________。图4610.如图46,梯形ABCD内接于⊙O,AD∥BC,过B引⊙O的切线分别交DA、CA的延长线于E、F.已知BC=8,CD=5,AF=6,则EF的长为________.图4711.(2013·衡阳模拟)如图47所示,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为________.解析及答案1.【解析】在Rt△ABC中,∵∠ACB=90°,CD⊥AB,3∴CD2=AD·DB.又CD是圆的切线,故CD2=CE·CB.∴CE·CB=AD·DB.【答案】①2.【解析】连接OC,则由PC是切线知OC⊥PC.由∠CAP=30°,知∠COP=60°,故∠CPA=30°.因为PC=2.∴OC=2=r,∴AB=4.【答案】43.【解析】由题意知OP⊥AB,且AP=a,根据相交弦定理AP2=CP·PD,CP=a.【答案】a4.【解析】由题意知∠BAC=90°,则∠PAC=120°-90°=30°,由弦切角定理知,∠B=30°,∴BC=2AC=4,∴圆O的面积S=4π.【答案】4π5.【解析】当D为AB中点时,OD⊥AB,OD最小,此时CD最大,所以CD最大值=AB=2.【答案】26.【解析】∵AB为直径,∴∠ACB=90°.又AB=,BC=,得AC=2.BD是圆O的切线,则AB⊥BD,由射影定理得BC2=AC·CD.故CD=1,所以AD=2+1=3.【答案】3二、填空题7.【解析】由题意知,AB=6,AE=1,∴BE=5.∴CE·DE=DE2=AE·BE=5.在Rt△DEB中,∵EF⊥DB,∴由射影定理得DF·DB=DE2=5.【答案】58.【解析】在△ADP与△CBP中,∠P=∠P.又四边形ABCD内接于圆O,∴∠PBC=∠ADP.因此△ADP∽△CBP,∴=,又∵PB=1,PD=3,∴=.【答案】9.【解析】由圆周角定理,及AD=DE,∴∠ABD=∠DBE,∠DBE=∠DAE,4则∠ABD=∠DAE,又AB为圆的直径,则∠ADB=90°,则△ADC∽△BDA,故=,则==.【答案】10.【解析】∵BE切⊙O于B,∴∠ABE=∠ACB.又AD∥BC,∴∠EAB=∠ABC,∴△EAB∽△ABC,∴=.又AE∥BC,∴=,∴=.又AD∥BC,∴AB=CD,∴AB=CD,∴=,∴=,∴EF==.【答案】11.【解析】如图,连接AB,AC,CE,由于A,E为半圆周上的三等分点,可得∠FBD=30°,∠ABD=60°,∠ACB=30°.由此得AB=2,AD=,BD=1,则DF=,故AF=.【答案】5