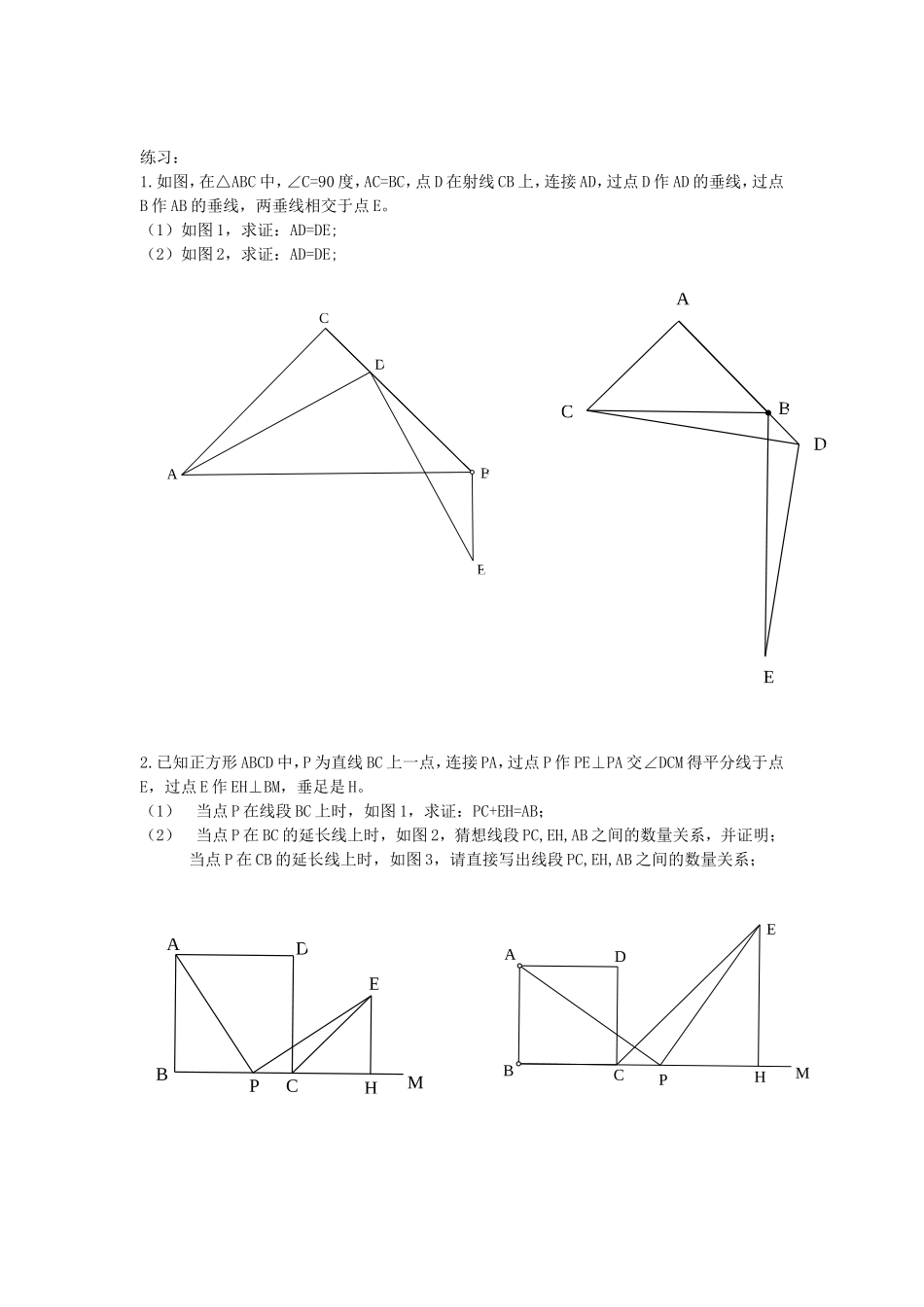
HKGFEDCBANCMEFGKHHKGFEDCBA教材基本图形变式教材原型如图l,四边形ABCD是正方形,且E是BC边的中点,∠AEF=90°,EF交正方形外角的平分线CK于F.求证:AE=EF.图1【变式一】若将例题中的条件“E是BC边的中点”,改为“E是BC边上的任意一点”,而其它条件保持不变,求证:AE=EF事实上,仍可运用例题的证明方法,推出结论,证明略.想一想:若将“点E在BC边上”的条件,改为“点E在直线BC上”,而其它条件不变,上述结论是否成立呢?【变式二】如图2,在“变式一”的条件下,过点F作FG⊥EF,交CD的延长线于G.求证:EF=FG.图2图3【变式三】如图3,在Rt△ECG中,∠ECG=90°,且点F是Rt△ECG外角平分线CK上一点,且FE=FG.(1)若CE=3,点F到直线EC的距离为1,则求CG的长。(2)若没有给出图,问题(1)中答案唯一吗?(3)猜想:CG、CE,CF之间的数量关系,并给出你的证明.FCHNKGMEKFEDCBA【变式四】如图4,在△EGC中,∠ECG=60°,点F是△ECG的外角平分线CK上一点,且FE=FG.试猜想:CG、CE、CF之间的数量关系.并给出你的证明.图4【变式五】在△EGC中,∠ECG=,点F是△ECG的外角平分线CK上一点,且FE=FG.试猜想:CG、CE、CF之间的数量关系.并给出你的证明.事实上,运用类似的证明方法,可得:CG-CE=2CFcos(90°-)【变式六】如图5,四边形ABCD是矩形,∠AEF=90°,AD:AB=5:3,BE:CE=1:4,EF交矩形形外角的平分线CK于F.(1)判断EF与AE之间的数量关系,并证明结论;(2)判断AB、CE、CF之间的数量关系,并证明结论。图5EDBACEDCBAHMPECDBAHMPECDBA练习:1.如图,在△ABC中,∠C=90度,AC=BC,点D在射线CB上,连接AD,过点D作AD的垂线,过点B作AB的垂线,两垂线相交于点E。(1)如图1,求证:AD=DE;(2)如图2,求证:AD=DE;2.已知正方形ABCD中,P为直线BC上一点,连接PA,过点P作PE⊥PA交∠DCM得平分线于点E,过点E作EH⊥BM,垂足是H。(1)当点P在线段BC上时,如图1,求证:PC+EH=AB;(2)当点P在BC的延长线上时,如图2,猜想线段PC,EH,AB之间的数量关系,并证明;当点P在CB的延长线上时,如图3,请直接写出线段PC,EH,AB之间的数量关系;3.如图,四边形ABCD是正方形,一直角三角板的直角顶点E在射线CB上滑动(点E不与点C、B重合),直角三角板的另一边与顶点与点A重合,一条直角边与∠DCM的平分线CF所在直线相交于点F。⑴如图1,当点E滑动到BC边的中点位置时,求证:AE=EF;⑵如图2,图3所示,当点E在BC边上滑动到任意位置,或点E在CB延长线上滑动时,请问⑴中结论是否成立,若成立,请你用图3证明;若不成立,请说明理由;FEDMCBAFEDMCBA