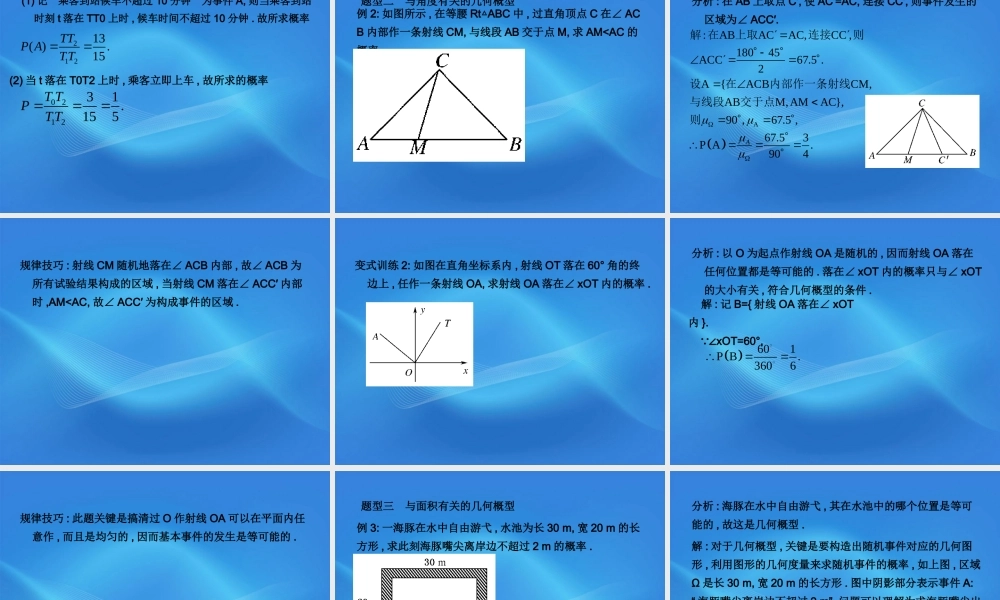
§3.3 几何概型3.3.1 几何概型 自 学 导 引1. 正确理解几何概型的概念 .2. 掌握几何概型的概率公式 .3. 会根据古典概型与几何概型的区别与联系来判别某种概型是古典概型还是几何概型 . 课 前 热 身 1. 如果每个事件发生的概率只与构成该事件区域的长度 ( 面积或体积 ) 成比例 , 则称这样的概率模型为 ____________, 简称 __________.2. 在几何概型中 , 事件 A 的概率定义为 ________, 习惯上 ,用 μA 表示事件 A 的区域几何度量 , 用 μΩ 表示试验的全部结果所构成区域的几何度量 .几何概率模型 几何概型 ( )AP A 名 师 讲 解 1. 几何概型试验的两个基本特征(1) 无限性 , 在一次试验中 , 可能出现的结果有无限多个 ;(2) 等可能性 , 每个结果的发生具有等可能性 .2. 几何概型的计算公式几何概型的试验中 , 事件 A 的概率 P(A) 只与子区域 A 的几何度量 ( 长度 面积或体积、) 成正比 , 而与 A 的位置和形状无关 . 因此有 AP A 构成事件 的区域长度 面积或体积实验的全部结果所构成的区域长度 面积或体积 3. 几何概型的计算步骤(1) 判断几何概型 , 尤其是判断等可能性 , 比古典概型更难于判断 .(2) 计算基本事件空间与事件 A 所含的基本事件对应的区域的几何度量 ( 长度 面积或体积、). 这是计算的难点 , 实际上教材重点不在于计数 , 而在于如何利用几何概型 , 把问题转化为各种几何概型问题 , 为此可参考如下办法 :① 适当选择观察角度 ;② 把基本事件空间转化为与之对应的区域 ;③ 对立事件逆向思维 ;④ 利用概率公式计算 . 典 例 剖 析 题型一 与长度有关的几何概型例 1: 取一根长为 5 m 的绳子 , 拉直后在任意位置剪断 , 那么剪得两段的长都不少于 2 m 的概率有多大 ?分析 : 从每一个位置剪断都是一个基本事件 , 剪断位置可以是长度为 5 m 的绳子上的任意一点 , 其基本事件有无限多个 , 显然不能用古典概型计算 , 可考虑运用几何概型计算 . 解 : 如图所示 . 记“剪得两段绳长都不小于 2 m” 为事件 A.把绳子五等分 , 于是当剪断位置处在中间一段上时 , 事件A 发生 . 由于中间一段的长度等于绳长的 所以事件A 发生的概率1 ,51( ).5P A 规律技巧 : 解答本类问题的关键是将基本事件的全部及其事件 A 包含的基本事件转化为相应的...