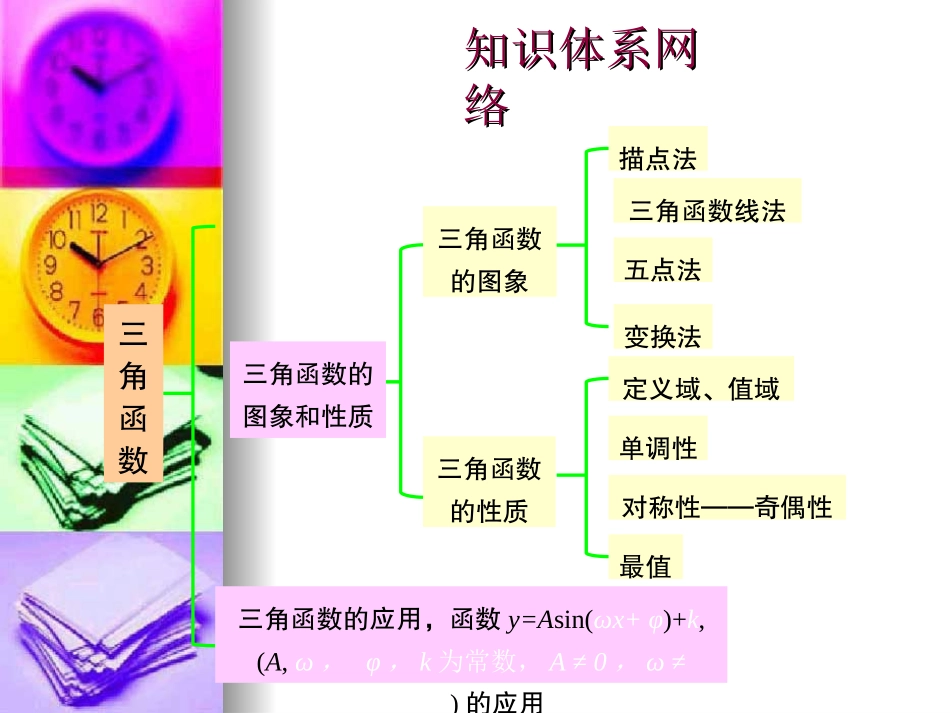
知识体系网知识体系网络络三角函数概念念三角函数同角三角函数关系任意角、弧度制任意角的三角函数诱导公式任意角的三角函数弧度制与角度制的互换弧度制任意角知识体系网知识体系网络络三角函数对称性——奇偶性三角函数的图象三角函数的性质最值定义域、值域三角函数线法描点法三角函数的图象和性质变换法五点法单调性三角函数的应用,函数y=Asin(ωx+φ)+k,(A,ω,φ,k为常数,A≠0,ω≠0,)的应用高考热点探高考热点探究究三角函数图象的难点在于三角函数图象三角函数图象的难点在于三角函数图象的变换.要突破这一难点,就要熟知三角的变换.要突破这一难点,就要熟知三角函数图象变换的一般方式:先作周期变换、函数图象变换的一般方式:先作周期变换、再作相位变换,也可以先作相位变换、再再作相位变换,也可以先作相位变换、再作周期变换.同时要注意的是:若先作周作周期变换.同时要注意的是:若先作周期变换,得到函数期变换,得到函数yy==sinsinωxωx的图象,再的图象,再作相位变换,将所得函数的图象向左作相位变换,将所得函数的图象向左((φφ>0)>0)或向右或向右((φφ<0)<0)平移平移||φφ||个单位长度,个单位长度,得到函数得到函数yy==sinsinωω((xx++φφ))的图象.这一的图象.这一点是我们常常出错之处,应该引起注意.点是我们常常出错之处,应该引起注意.三角函数的图象及其变换热点一高考热点探高考热点探究究【【思路点拨思路点拨】】先将函数变形为先将函数变形为yy==AAsin(sin(ωxωx++φφ))++BB的的形式,再运用函数图象变换.在进行函数图象变换中,形式,再运用函数图象变换.在进行函数图象变换中,有以下两种方式,即先进行平移变换,再进行伸缩变有以下两种方式,即先进行平移变换,再进行伸缩变换;或先进行伸缩变换,再进行平移变换.换;或先进行伸缩变换,再进行平移变换.例例11已知函数y=12cos2x+32sinxcosx+1(x∈R),该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到.高考热点探高考热点探究究解】法一:y=12cos2x+32sinxcosx+1=14(2cos2x-1)+14+34(2sinxcosx)+1=14cos2x+34sin2x+54=12(cos2xsinπ6+sin2xcosπ6)+54=12sin(2x+π6)+54.高考热点探高考热点探究究将y=sinx向左平移π6个单位长度得y=sin(x+π6),再把所得图象上所有点的横坐标变为原来的12倍得y=sin(2x+π6),再把所得图象上所有点的纵坐标变为原来的12倍,得y=12sin(2x+π6),再把函数图象向上平移54个单位长度,得y=12sin(2x+π6)+54.高考热点探高考热点探究究法二:化简同上,y=12sin(2x+π6)+54.将y=sinx横坐标缩小为原来的12倍得y=sin2x,再把函数图象向右平移π12个单位长度得y=sin2(x+π12),再将纵坐标缩小为原来的12倍得y=12sin2(x+π12),再将所得函数图象向上平移54个单位长度得y=12sin2(x+π12)+54=12sin(2x+π6)+54.高考热点探高考热点探究究【点评】本题是一个函数图象变换的问题,其难点在于对两种变换方式的把握.要突破这一难点,就要掌握这两种变换的规律,即先相位变换、再周期变换(如法一),或先周期变换、再相位变换(如法二).而先周期变换,再相位变换时,要注意的是由y=sin2x的图象向左平移π12(而不是π6)个单位长度,得到y=sin2(x+π12)的图象.这也就是说,将函数y的图象沿着x轴左右平移时,是在x后边加减.这是这类问题最容易出现错误的地方,我们要给予重视.高考热点探高考热点探究究三角函数与图象相关的性质:三角函数三角函数与图象相关的性质:三角函数yy==AAsin(sin(ωxωx++φφ))的图象在其对称轴处取到最大值或最小值,且相的图象在其对称轴处取到最大值或最小值,且相邻的最大值与最小值之间的距离为其函数的半个周邻的最大值与最小值之间的距离为其函数的半个周期;函数图象与期;函数图象与xx轴的交点是其对称中心,相邻两轴的交点是其对称中心,相邻两对称中心之间的距离也是函数的半个周期;函数取对称中心之间的距离也是函数的半个周期;函数取最值的点与相邻的最值的点与相邻的xx轴的交点之间的距离为其函数轴的交点之间的距离为其...