九年级数学动点问题课件VIP免费

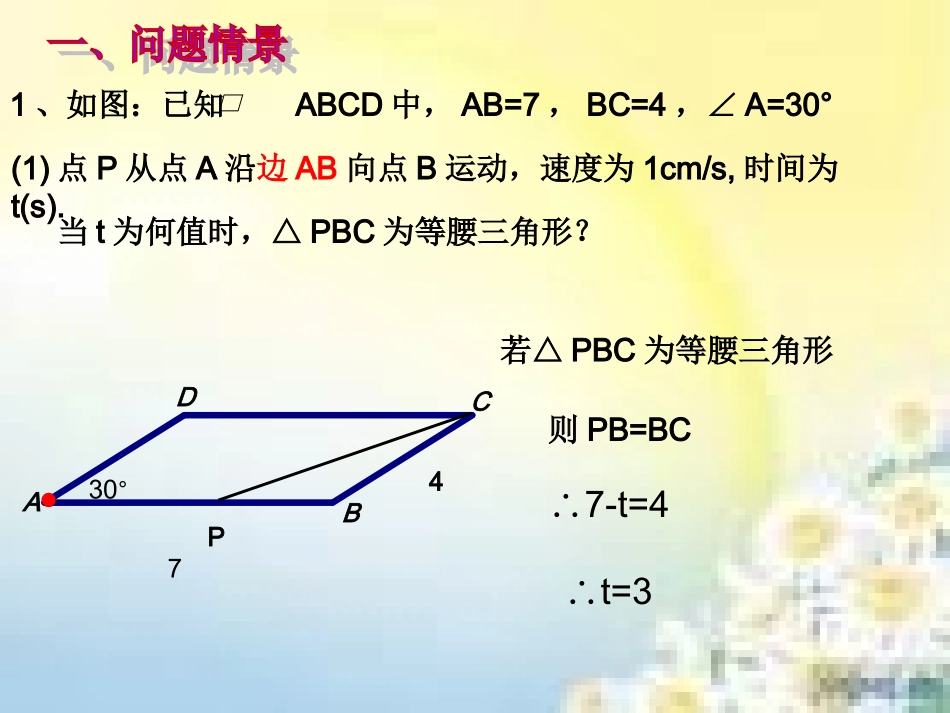
九年级动点问题解析最后一题并不可怕，更要有信心！图形中的点、线运动，构成了数学中的一个新问题----动态几何。它通常分为三种类型：动点问题、动线问题、动形问题。在解这类问题时，要充分发挥空间想象的能力，不要被“动”所迷惑，而是要在“动”中求“静”，化“动”为“静”，抓住它运动中的某一瞬间，寻找确定的关系式，就能找到解决问题的途径。本节课重点来探究动态几何中的第一种类型----动点问题。1、如图：已知ABCD中，AB=7，BC=4，∠A=30°DCBA(1)点P从点A沿边AB向点B运动，速度为1cm/s,时间为t(s).7430°P当t为何值时，△PBC为等腰三角形？若△PBC为等腰三角形则PB=BC∴7-t=4∴t=3如图：已知ABCD中，AB=7，BC=4，∠A=30°当t为何值时，△PBC为等腰三角形？PDCBA74(2)若点P从点A沿AB运动，速度仍是1cm/s。射线小组合作交流讨论PDCBA74当BP=BC时（锐角)PDCBA7430°当CB=CP时∟E32P当PB=PC时DCBA74PEDCBA74当BP=BC时（钝角）1、如图：已知ABCD中，AB=7，BC=4，∠A=30°PDCBA74当BP=BC时PDCBA7430°当CB=CP时∟E32P当PB=PC时DCBA74PEDCBA74当BP=BC时(2)若点P从点A沿射线AB运动，速度仍是1cm/s。当t为何值时，△PBC为等腰三角形？探究动点关键：化动为静，分类讨论，关注全过程(2)若点P从点A沿射线AB运动，速度仍是1cm/s。当t为何值时，△PBC为等腰三角形？PDCBA74当BP=BC时(钝角)当BP=BC时(锐角)当CB=CP时当PB=PC时∴t=3或11或7+或/3+7时△PBC为等腰三角形34341.如图：已知ABCD中，AB=7，BC=4，∠A=30°DCBA（3）当t＞7时，是否存在某一时刻t,使得线段DP过线段BC的三等分点？PEPEDCBA解决动点问题的好助手：数形结合定相似比例线段构方程（1）当t为何值时，PQBC?∥CBAPDQ2.在RtABC△中，∠C=90°，AC=6cm，BC=8cm，点P由点A出发，沿AC向C运动，速度为2cm/s，同时点Q由AB中点D出发，沿DB向B运动，速度为1cm/s，连接PQ，若设运动时间为t(s)(0＜t≤3)若PQBC∥62105tt715tACAPABAQ则△AQP～△ABC2t5+t(2)设△APQ的面积为y()，求y与t之间的函数关系。2cm∟M∟N2.在RtABC△中，∠C=90°，AC=6cm，BC=8cm，点P由点A出发，沿AC向C运动，速度为2cm/s，同时点Q由AB中点D出发，沿DB向B运动，速度为1cm/s，连接PQ，若设运动时间为t(s)(0＜t≤3)CBAPDQCBAPDQ∟NCBAPDQttytty4545442212 △AQNABC∽△1058tQNtQN544ABAQBCQN相似法2.(2)N∟CBAPDQtQN54490CABCRt中，在108AQQN1085tQN108SinA三角函数法2.(2)ttytty45454422122.(3)是否存在某一时刻t，使△APQ的面积与△ABC的面积比为7︰15？若存在，求出相应的t的值；不存在说明理由。∴当t=2时，△APQ的面积与△ABC的面积比为7︰15246821ABCS157ABCSy241574542tt01452tt0)2)(7(tt2,(7tt舍去）CBAPDQ计算要仔细2.（4）连接DP,得到△QDP，那么是否存在某一时刻t，使得点D在线段QP的中垂线上？若存在，求出相应的t的值；若不存在，说明理由。 点D在线段PQ的中垂线上∴DQ=DP22DPDQ222)32(4tt0251232tt∴方程无解。即点D都不可能在线段QP的中垂线上。 △=—156<0∟GCBAPDQt2t34.4.（2009中考）例1、如图，已知在直角梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，BC=26cm，动点P从点A开始沿AD边向点D，以1cm/秒的速度运动，动点Q从点C开始沿CB向点B以3厘米/秒的速度运动，P、Q分别从点A点C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒，求：1）t为何值时，四边形PQCD为平行四边形2)t为何值时，等腰梯形？1t3t24264(1)解：要使四边形PQCD为平行四边形，只要QC=PD∴3t=24-t∴t=6，∴当t=6秒时，四边形PQCD为平行四边形1t3t2426由题意，只要PQ=CD，则四边形PQCD为等腰梯形┐F┌E过P、D分别作BC的垂线交BC于E、F:4.2)解：t3t则EF=PD，QE=FC=2∴t=7，∴当t=7秒时，四边形PQCD为等腰梯形。∴3t--4=24--t455545.如图(1):在梯形ABCD中:AD=BC=5cm,AB=4cm,CD=10cm,BEAD∥。如图(2):若整个△BEC从点E以1cm/s的速度沿射线CD平移，同时...