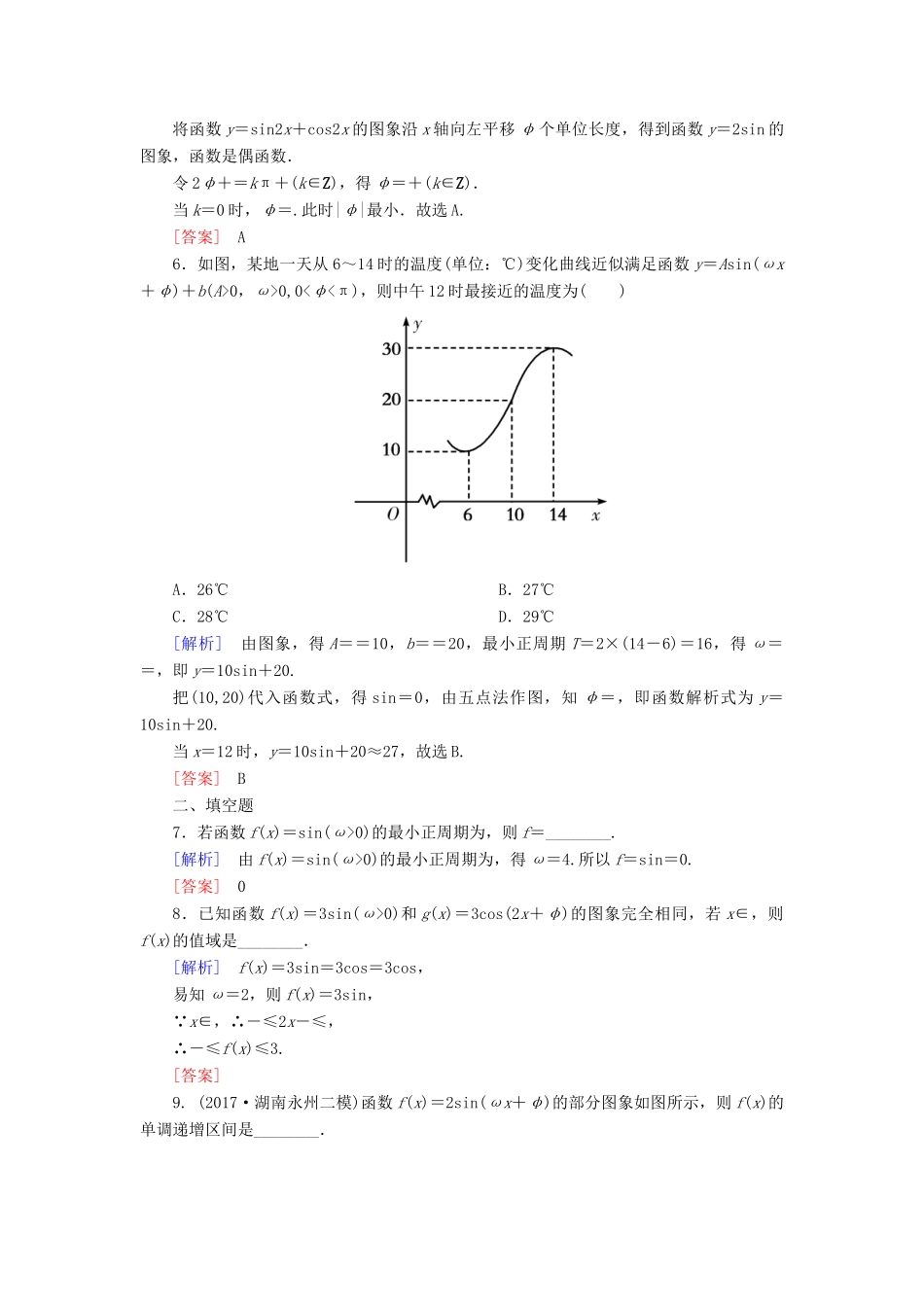
课时跟踪训练(二十二)函数y=Asin(ωx+φ)的图象及应用[基础巩固]一、选择题1.(2018·湖南张家界一中月考)为了得到f(x)=2sin的图象,只需将g(x)=2sinx的图象()A.纵坐标不变,横坐标伸长为原来的3倍,再将所得图象向右平移个单位长度B.纵坐标不变,横坐标伸长为原来的3倍,再将所得图象向右平移个单位长度C.纵坐标不变,横坐标缩短为原来的,再将所得图象向右平移个单位长度D.纵坐标不变,横坐标缩短为原来的,再将所得图象向右平移个单位长度[解析]将g(x)=2sinx的图象的纵坐标不变,横坐标缩短为原来的,得y=2sin3x的图象;再将所得图象向右平移个单位长度,得f(x)=2sin3=2sin的图象.故选D.[答案]D2.若函数f(x)=2sin(ωx+φ),x∈R的最小正周期是π,且f(0)=,则()A.ω=,φ=B.ω=,φ=C.ω=2,φ=D.ω=2,φ=[解析]由T==π,∴ω=2.由f(0)=⇒2sinφ=,∴sinφ=,又|φ|<,∴φ=.[答案]D3.(2018·河南平顶山模拟)为得到函数y=cos的图象,只需将函数y=sinx的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位[解析]因为y=cos=sin=sin.故其图象可以看作函数y=sinx的图象向左平移个长度单位而得到.[答案]C4.为了使函数y=sinωx(ω>0)在区间[0,1]上至少出现50次最大值,则ω的最小值是()A.98πB.πC.πD.100π[解析]设函数的最小正周期为T,由题意知T≤1,即×≤1,∴ω≥.[答案]B5.将函数y=sin2x+cos2x的图象沿x轴向左平移φ个单位长度后,得到一个偶函数的图象,则|φ|的最小值为()A.B.C.D.[解析]函数y=sin2x+cos2x=2sin,将函数y=sin2x+cos2x的图象沿x轴向左平移φ个单位长度,得到函数y=2sin的图象,函数是偶函数.令2φ+=kπ+(k∈Z),得φ=+(k∈Z).当k=0时,φ=.此时|φ|最小.故选A.[答案]A6.如图,某地一天从6~14时的温度(单位:℃)变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则中午12时最接近的温度为()A.26℃B.27℃C.28℃D.29℃[解析]由图象,得A==10,b==20,最小正周期T=2×(14-6)=16,得ω==,即y=10sin+20.把(10,20)代入函数式,得sin=0,由五点法作图,知φ=,即函数解析式为y=10sin+20.当x=12时,y=10sin+20≈27,故选B.[答案]B二、填空题7.若函数f(x)=sin(ω>0)的最小正周期为,则f=________.[解析]由f(x)=sin(ω>0)的最小正周期为,得ω=4.所以f=sin=0.[答案]08.已知函数f(x)=3sin(ω>0)和g(x)=3cos(2x+φ)的图象完全相同,若x∈,则f(x)的值域是________.[解析]f(x)=3sin=3cos=3cos,易知ω=2,则f(x)=3sin, x∈,∴-≤2x-≤,∴-≤f(x)≤3.[答案]9.(2017·湖南永州二模)函数f(x)=2sin(ωx+φ)的部分图象如图所示,则f(x)的单调递增区间是________.[解析]由函数f(x)的图象,得T=-=,∴T==π,∴ω=2.又 函数f(x)的图象经过,∴2=2sin,∴+φ=2kπ+,k∈Z,即φ=2kπ-,k∈Z.又 -<φ<,∴φ=-,∴f(x)=2sin.由2kπ-≤2x-≤2kπ+,k∈Z,解得f(x)的单调增区间是,k∈Z.[答案],k∈Z三、解答题10.(2017·郴州模拟)已知函数f(x)=sin(ω>0)的最小正周期为π.(1)求ω的值,并在下面提供的坐标系中画出函数y=f(x)在区间[0,π]上的图象;(2)函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换得到?[解](1)f(x)=sin,因为T=π,所以=π,即ω=2,故f(x)=sin.列表如下:2x+π2πx0πf(x)10-10y=f(x)在[0,π]上的图象如图所示.(2)将y=sinx的图象上的所有点向左平移个单位长度,得到函数y=sin的图象.再将y=sin的图象上所有点的横坐标缩短到原来的(纵坐标不变),得到函数f(x)=sin(x∈R)的图象.[能力提升]11.(2017·贵州省贵阳市高三监测)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导数f′(x)的图象如图所示,则f的值为()A.2B.C.-D.-[解析]依题意得f′(x)=Aωcos(ωx+φ),结合函数y=f′(x)的图象可知,T==4=π,ω=2.又Aω=1,因此A=.因为0<φ<π,<+φ<,且f′=cos=-1,所以+φ=π,解得φ=,故f(x)=sin,...