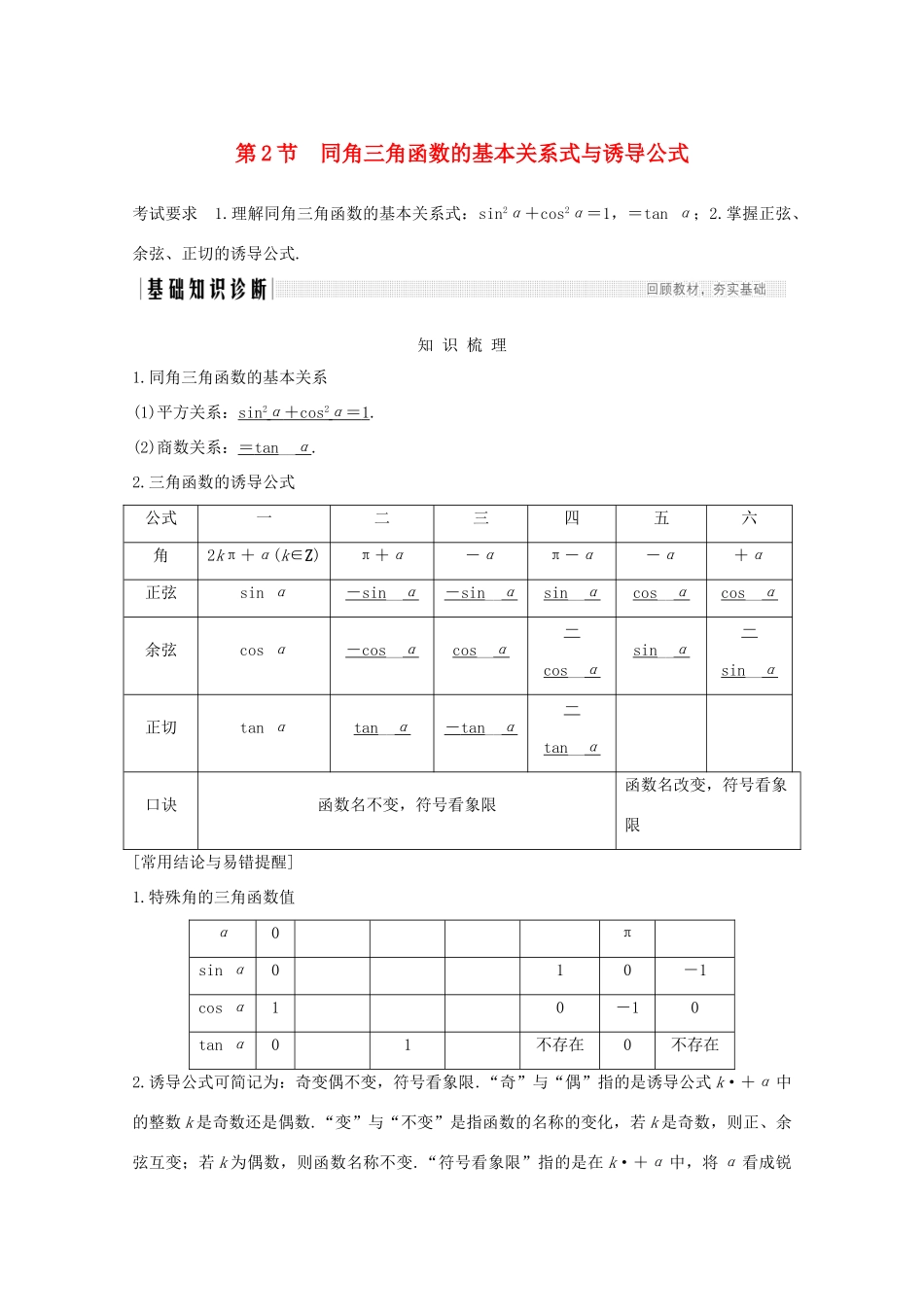
第2节同角三角函数的基本关系式与诱导公式考试要求1.理解同角三角函数的基本关系式:sin2α+cos2α=1,=tanα;2.掌握正弦、余弦、正切的诱导公式.知识梳理1.同角三角函数的基本关系(1)平方关系:sin2α+cos2α=1.(2)商数关系:=tan__α.2.三角函数的诱导公式公式一二三四五六角2kπ+α(k∈Z)π+α-απ-α-α+α正弦sinα-sin__α-sin__αsin__αcos__αcos__α余弦cosα-cos__αcos__α-cos__αsin__α-sin__α正切tanαtan__α-tan__α-tan__α口诀函数名不变,符号看象限函数名改变,符号看象限[常用结论与易错提醒]1.特殊角的三角函数值α0πsinα010-1cosα10-10tanα01不存在0不存在2.诱导公式可简记为:奇变偶不变,符号看象限.“奇”与“偶”指的是诱导公式k·+α中的整数k是奇数还是偶数.“变”与“不变”是指函数的名称的变化,若k是奇数,则正、余弦互变;若k为偶数,则函数名称不变.“符号看象限”指的是在k·+α中,将α看成锐角时k·+α所在的象限.诊断自测1.判断下列说法的正误.(1)sin(π+α)=-sinα成立的条件是α为锐角.()(2)六组诱导公式中的角α可以是任意角.()(3)诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.()(4)若sin(kπ-α)=(k∈Z),则sinα=.()解析(1)对于α∈R,sin(π+α)=-sinα都成立.(4)当k为奇数时,sinα=,当k为偶数时,sinα=-.答案(1)×(2)√(3)√(4)×2.sin600°的值为()A.-B.-C.D.解析sin600°=sin(360°+240°)=sin240°=sin(180°+60°)=-sin60°=-.答案B3.已知sin=-,α∈,则tanα=()A.B.-C.-D.解析sin=cosα=-,又α∈,则sinα==,则tanα==-,故选C.答案C4.已知sinθ+cosθ=,θ∈,则sinθ-cosθ的值为()A.B.-C.D.-解析 sinθ+cosθ=,∴1+2sinθcosθ=,∴sinθcosθ=.又 (sinθ-cosθ)2=1-2sinθcosθ=,又 θ∈,∴sinθ-cosθ=-.答案B5.(必修4P22B3改编)已知tanα=2,则的值为________.解析原式===3.答案36.设a为常数,且a>1,0≤x≤2π,则当x=________时,函数f(x)=cos2x+2asinx-1的最大值为________.解析f(x)=cos2x+2asinx-1=1-sin2x+2asinx-1=-(sinx-a)2+a2,因为0≤x≤2π,所以-1≤sinx≤1,又因为a>1,所以当sinx=1,即x=时,f(x)max=-(1-a)2+a2=2a-1.答案2a-1考点一同角三角函数基本关系式的应用【例1】(1)(2020·浙江教育绿色评价联盟适考)已知α为第二象限角,且3sinα+cosα=0,则sinα=()A.B.C.-D.-(2)已知sinαcosα=,且<α<,则cosα-sinα的值为()A.-B.C.-D.(3)若tanα=,则cos2α+2sin2α=()A.B.C.1D.解析(1)由3sinα=-cosα,两边平方得9sin2α=1-sin2α,则sinα=±,又α为第二角限角,所以sinα>0,则sinα=,故选A.(2) <α<,∴cosα<0,sinα<0且cosα>sinα,∴cosα-sinα>0.又(cosα-sinα)2=1-2sinαcosα=1-2×=,∴cosα-sinα=.(3)tanα=,则cos2α+2sin2α===.答案(1)A(2)B(3)A规律方法(1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tanα可以实现角α的弦切互化.(2)应用公式时注意方程思想的应用:对于sinα+cosα,sinαcosα,sinα-cosα这三个式子,利用(sinα±cosα)2=1±2sinαcosα,可以知一求二.(3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.【训练1】(1)已知sinα-cosα=,α∈(0,π),则tanα=()A.-1B.-C.D.1(2)若3sinα+cosα=0,则的值为()A.B.C.D.-2(3)已知sinα=,0<α<π,则tanα=__________,sin+cos=__________.解析(1)由得:2cos2α+2cosα+1=0,即=0,∴cosα=-.又α∈(0,π),∴α=,∴tanα=tan=-1.(2)3sinα+cosα=0⇒cosα≠0⇒tanα=-,====.(3)因为0<α<π,所以tanα==±=±=±,又0<<,所以sin>0,cos>0,所以sin+cos====.答案(1)A(2)A(3)±考点二诱导公式的应用【例2】(1)化简:sin(-1200°)cos1290°+cos(-1020°)...