2216平行线分线段成比例定理VIP免费

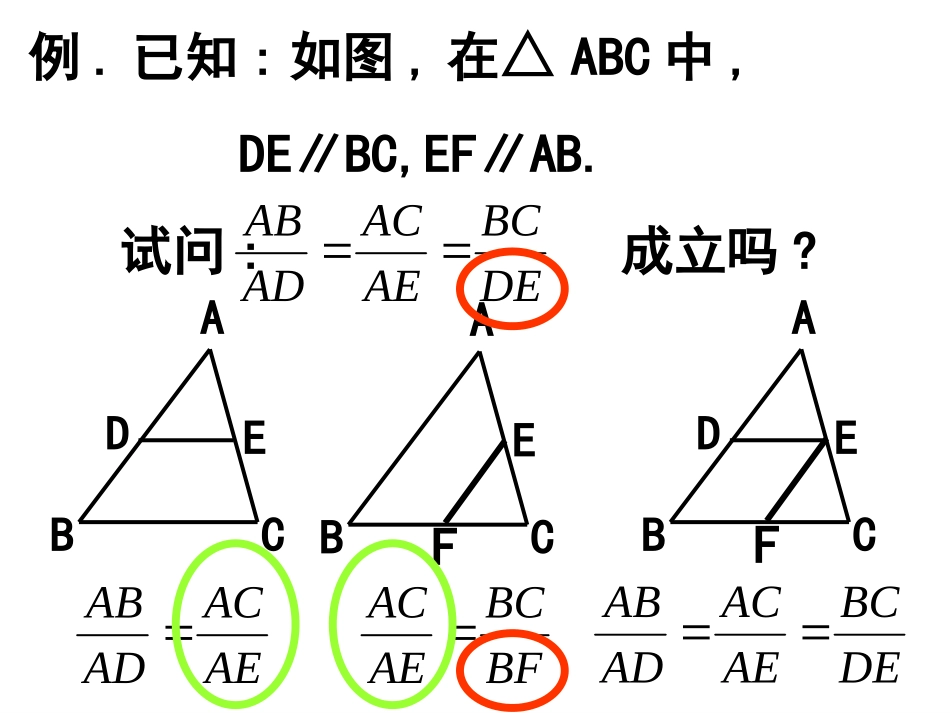
平行线分线段成比例定理例.已知:如图,在△ABC中,DE∥BC,EF∥AB.试问:成立吗?DEBCAEACADABABCDEFABCEFABCDEAEACADABBFBCAEACDEBCAEACADAB练：如图,△ABC中,DF//AC,DE//BC,AE=4,EC=2,BC=8.求BF和CF的长.FACB解∵DE//BC3264ACAEABAD∵DF//ACCBCFABAD316,832CFCF即38316-8BFDE练：如图,△ABC中,DE//BC,EF//CD.求证:AD是AB和AF的比例中项.FEBACD证明,,ABACABCDE//BCADAE在中,,ADACADCEF//CDAFAE在中ABADADAF∴AD2=ABAF,即AD是AB和AF的比例中项•已知线段a、b，求作线段x，使x=，正确的作法是（）22ba课本P72T6、7AABBCCDDEEFFll11ll33ll22123综上所述：若l//l//l,则：ABDEBCEFBCEFABDEABDEACDFBCEFACDF下下上上上上下下上上全全下下全全................形象记忆形象记忆•如果两条直线被一组平行线所截呢？1kknAAAA两条直线被三条平行线所截，所得的对应线段成比例。l1l2ln-1l3lklnA1AkAnB1BkBnA2B2A3B3An-1Bn-11kknBBBB平行线分线段成比例定理：两条直线被一组平行线所截，所得的对应线段成比例ab基本图形：“A”字形l1l2l3ABCDEFABDEBCEF部分线擦去,取一部分ab基本图形：“x”字形l1l2l3ABCD（E）FABDEBCEF部分线擦去,取一部分!注意:应用平行线分线段成比例定理得到的比例式中,四条线段与两直线的交点位置无关!ab平行线等分线段定理：两条直线被一组平行线所截，如果在一直线上所截得的线段相等，那么在另一直线上所截得的线段也相等。l1l2l3ABCDEFABDEBCEF平行线分线段成比例定理与平行线等分线段定理有何联系？ABCDEFABCDEFABBC当11当BCAB结论：后者是前者的一种特殊情况！结论：后者是前者的一种特殊情况！判断题1、若AB∥CD∥EF，ABCDEFAC=CE，则BD=DF=AC=CE.()×问题１：求作一点Ｐ把线段ＡＢ分成２：３问题２：如果把△ABC的面积分成２：３怎么办？例已知：线段ＡＢ求作：线段ＡＢ的五等分点ＡＢＣA2A3A4A5A1B1B2B3B4ＣP2、已知△ABC中，AB=AC，AD⊥BC，M是AD的中点，CM交AB于P，DN∥CM交AB于N，如果AB=6厘米，则PN=厘米.2ABCD.MPN∟3、已知：AD为△ABC的中线，ABCDMPM为AD的中点，直线CM交AB于点P，求证：AP=—13AB.证明：Q过点D作DQ∥CP交AB于点Q；