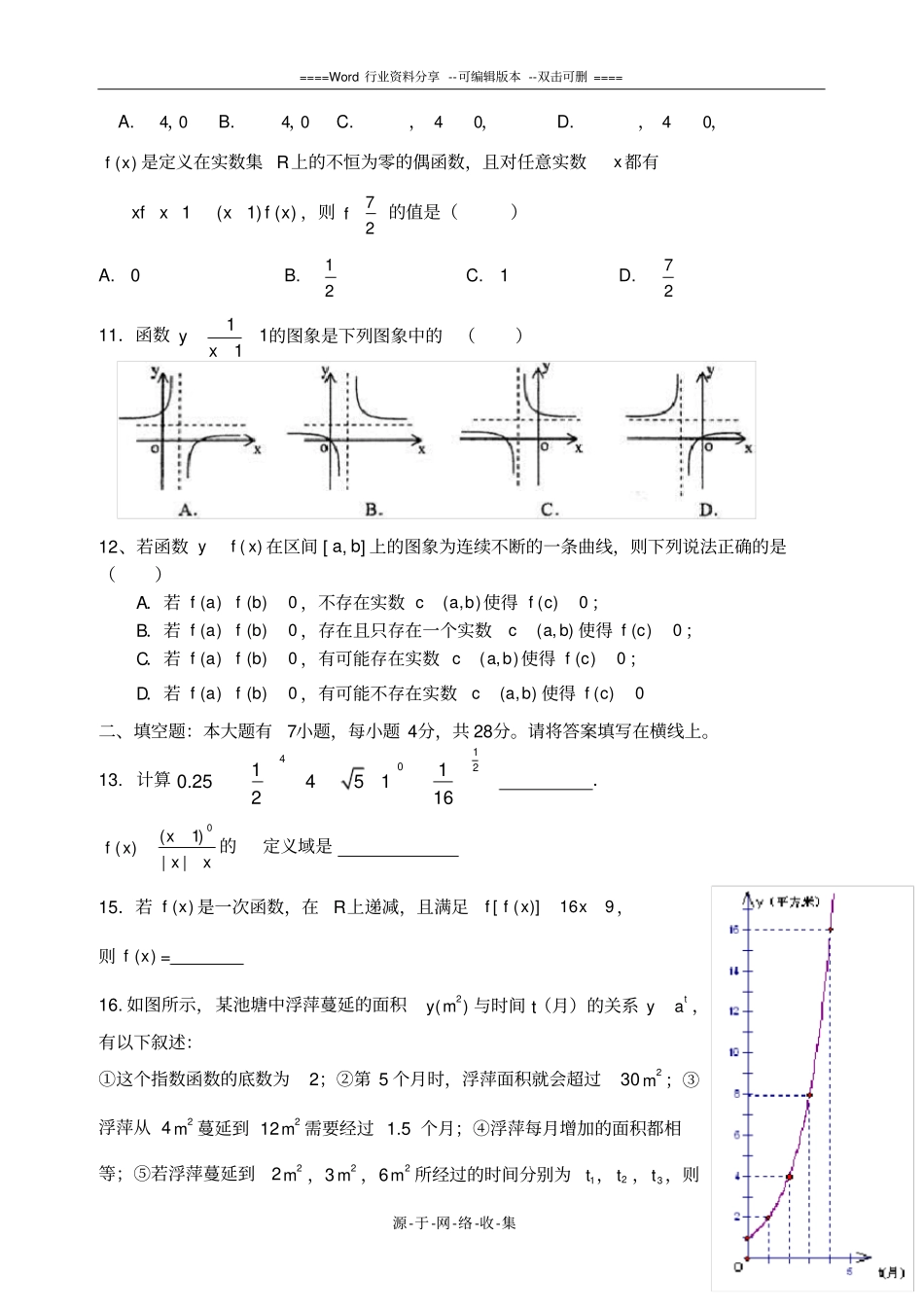
====Word行业资料分享--可编辑版本--双击可删====源-于-网-络-收-集高一数学11月期中模拟考试数学试卷一.选择题:(本大题共10小题,每题3分,共30分)1.已知全集U={1,2,3,4,5,6},A={1,2,3,4},B={3,4,5,6},那么CU(A∩B)=()A.{3,4}B.{1,2,5,6}C.{1,2,3,4,5,6}D.Φ2.下列图形中,不可作为函数)(xfy图象的是()3.若a∈R,则下列式子恒成立的是()A22nnmmaaB24aaC2()2()nnmmaaD5522aa4.下列各组中的两个函数是同一函数的为()A.3)5)(3(1xxxy,52xyB.111xxy,)1)(1(2xxyC.21)52()(xxf,52)(2xxfD.343()fxxx,3()1Fxxx5.已知函数f(x)的定义域是(1,2),则函数)2(xf的定义域是()A.)2,1(B.)4,2(C.)1,21(D.)1,0(axxxf2)(是偶函数,)(xg=xxb24是奇函数,那么ba的值为()A.1B.-1C.-21D.21①2xy,②1)21(xy,③|2|2xxy,④xxy1,其中在区间(0,1)上单调递减的函数序号是()A.①③B.②③C.②④D.①④)(xf为奇函数,且x)0.(时,)1()(xxxf,则x),0(时,)(xf为()A.)1(xxB.)1(xxC.)1(xxD.)1(xx9.对于集合M、N,定义)()(,|MNNMNMNxMxxNM且设RxxxyyM,4|2,RxyyNx,2|,则NM=()yxOAyxOByxOCyxOD====Word行业资料分享--可编辑版本--双击可删====源-于-网-络-收-集A.04,B.04,C.,,04D.,,04()fx是定义在实数集R上的不恒为零的偶函数,且对任意实数x都有1(1)()xfxxfx,则72f的值是()A.0B.12C.1D.7211.函数111xy的图象是下列图象中的()12、若函数)(xfy在区间[a,b]上的图象为连续不断的一条曲线,则下列说法正确的是()A.若0)()(bfaf,不存在实数),(bac使得0)(cf;B.若0)()(bfaf,存在且只存在一个实数),(bac使得0)(cf;C.若0)()(bfaf,有可能存在实数),(bac使得0)(cf;D.若0)()(bfaf,有可能不存在实数),(bac使得0)(cf二、填空题:本大题有7小题,每小题4分,共28分。请将答案填写在横线上。13.计算1402110.25451216.xxxxf||)1()(0的定义域是15.若)(xf是一次函数,在R上递减,且满足916)]([xxff,则)(xf=16.如图所示,某池塘中浮萍蔓延的面积2()ym与时间t(月)的关系tya,有以下叙述:①这个指数函数的底数为2;②第5个月时,浮萍面积就会超过302m;③浮萍从42m蔓延到122m需要经过1.5个月;④浮萍每月增加的面积都相等;⑤若浮萍蔓延到22m,32m,62m所经过的时间分别为1t,2t,3t,则====Word行业资料分享--可编辑版本--双击可删====源-于-网-络-收-集123ttt;其中正确的序号是三、解答题:本大题有5小题,共42分。解答应写出文字说明,证明过程或演算步骤。17.(本题满分12分)已知集合36Axx,29Bxx.(1)分别求RCAB,RCBA;(2)已知1axaxC,若BC,求实数a的取值集合.18.(12分)设4()4xxfxa,且()fx的图象过点11(,)22(1)求()fx表达式(2)计算()(1)fxfx(3)试求123201120112011fff2009201020112011ff的值19、(12分)已知二次函数f(x)满足f(x-3)=f(-x-3),且该函数的图像与y轴交于点(0,-1),在x轴上截得的线段长为62。(1)确定该二次函数的解析式;(2)当x∈[-6,-1]时,求f(x)值域。20.本题满分(12分)已知函数1515)(xxxf,1,1x(1)证明)(xf为奇函数.(2)判断)(xf在定义域上的单调性并证明.(3)解不等式)(xf)1(xf====Word行业资料分享--可编辑版本--双击可删====源-于-网-络-收-集21.(本题满分12分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式。(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能是企业获得最大利润,其最大利润为多少万元。22.(14分)设定义在R上的函数)(xf,对任意,,Ryx有)()()(yfxfyxf,且当0x时,恒有0)(xf,若2)1(f.(1)求)0(f;(2)判断该函数的奇偶性;(3)求证:Rx时)(xf为单调递增函数.(4)解不等式6)63(xf.