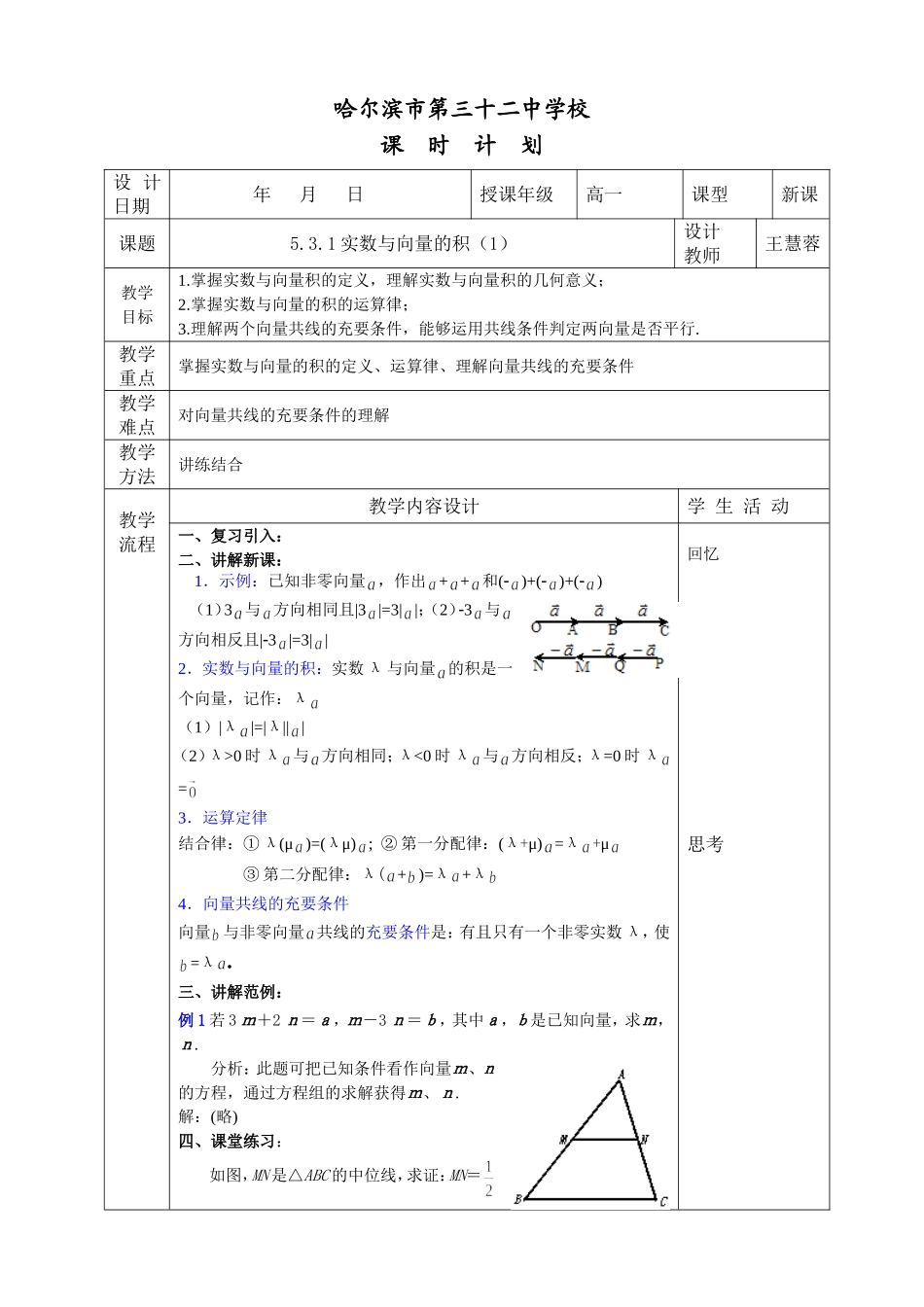
哈尔滨市第三十二中学校课时计划设计日期年月日授课年级高一课型新课课题5.3.1实数与向量的积(1)设计教师王慧蓉教学目标1.掌握实数与向量积的定义,理解实数与向量积的几何意义;2.掌握实数与向量的积的运算律;3.理解两个向量共线的充要条件,能够运用共线条件判定两向量是否平行.教学重点掌握实数与向量的积的定义、运算律、理解向量共线的充要条件教学难点对向量共线的充要条件的理解教学方法讲练结合教学流程教学内容设计学生活动一、复习引入:二、讲解新课:1.示例:已知非零向量,作出++和()+()+()(1)3与方向相同且|3|=3||;(2)3与方向相反且|3|=3||2.实数与向量的积:实数λ与向量的积是一个向量,记作:λ(1)|λ|=|λ|||(2)λ>0时λ与方向相同;λ<0时λ与方向相反;λ=0时λ=3.运算定律结合律:①λ(μ)=(λμ);②第一分配律:(λ+μ)=λ+μ③第二分配律:λ(+)=λ+λ4.向量共线的充要条件向量与非零向量共线的充要条件是:有且只有一个非零实数λ,使=λ奎屯王新敞新疆三、讲解范例:例1若3m+2n=a,m-3n=b,其中a,b是已知向量,求m,n.分析:此题可把已知条件看作向量m、n的方程,通过方程组的求解获得m、n.解:(略)四、课堂练习:如图,MN是△ABC的中位线,求证:MN=回忆思考BC,且MN∥BC.证明:∵M、N分别是AB、AC边上的中点,所以=,=,=-=-=(-)=.因此,NM=BC且MN∥BC.五、小结:通过本节学习,要求大家掌握实数与向量的积的定义,掌握实数与向量的积的运算律,理解两个向量共线的充要条件,并能在解题中加以运用.六、课后作业:1.当λÎZ时,验证:λ(+)=λ+λ2.如图,在△ABC中,=,=,AD为边BC的中线,G为△ABC的重心,求向量教学反思实数与向量的乘积仍是一个向量,这一点要多加强调。教务处查阅:DABMCMab