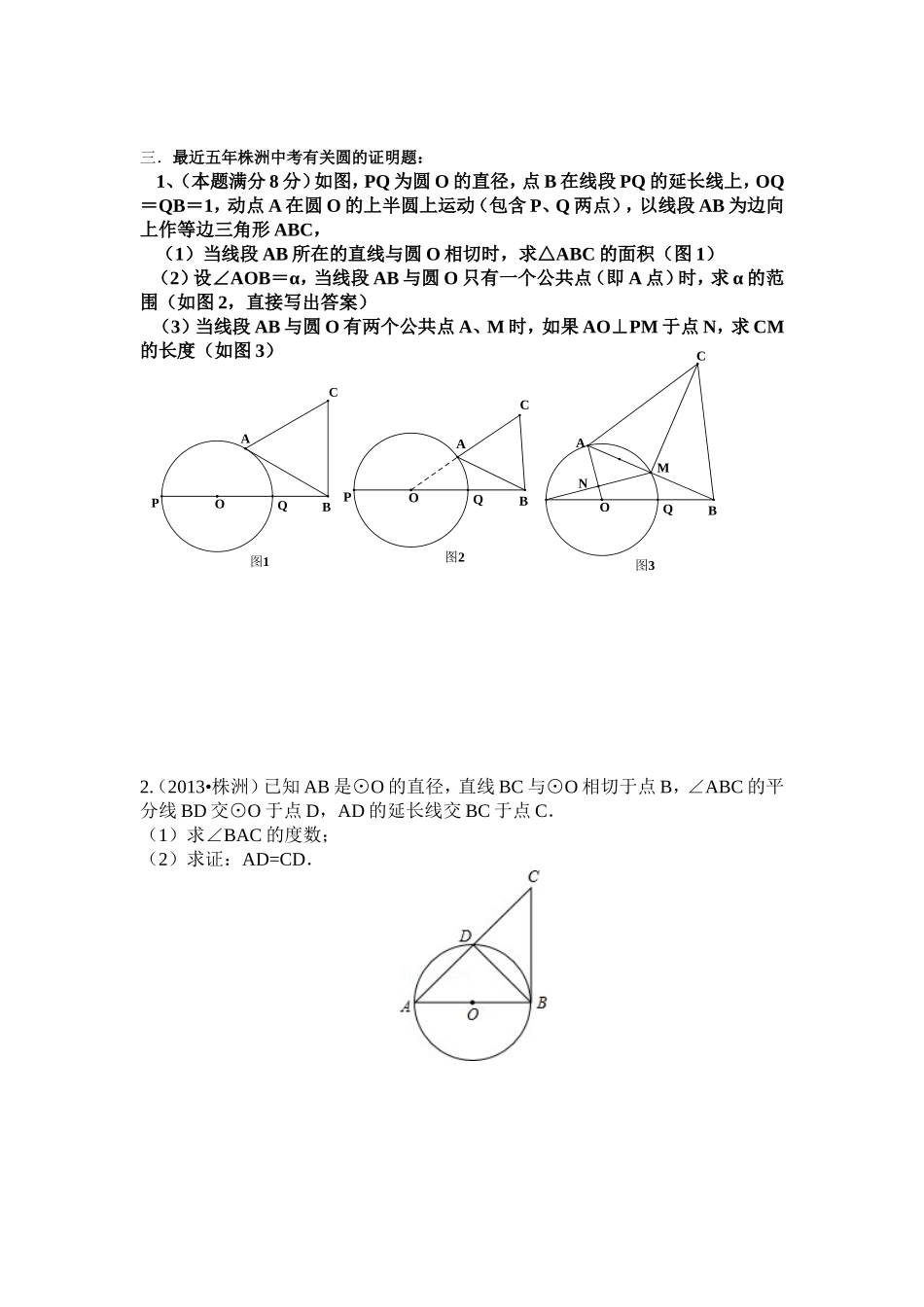
第11题图COBA株洲中考试题分析与总结:圆一.最近五年株洲中考数学试题情况:年份填空题证明题的内容分值2012年中考1小题切线的性质;全等三角形的判定;圆周角定理。8分2011年中考●切线的性质,圆周角定理的推论,垂径定理,三角函数8分2010年中考1小题切线的性质;全等三角形的判定;圆周角定理的推论。8分2009年中考1小题垂径定理,角平分线的判定,勾股定理,30°的Rt△。10分2008年中考●切线的性质;勾股定理,30°的Rt△,动点问题。7分二.最近五年株洲中考有关圆的填空选择题:特点:有三年出了填空题,没有出选择题。年份考试的内容分值2012年中考圆周角定理的考查3分2010年中考圆与圆的位置关系的考查3分2009年中考切线的性质和圆周角定理的考查3分1、(2014•株洲)如图,点A、B、C、都在圆O上,如果∠AOB+∠ACB=84°,那么∠ACB的大小是2.(2013•株洲)如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是48度3.(2012•株洲)已知:如下左图,在⊙O中,C在圆周上,∠ACB=45°,则∠AOB=_________.4.(2010年株洲)两圆的圆心距,它们的半径分别是一元二次方程的两个根,这两圆的位置关系是.5.(2009年株洲)如上右图,是⊙O的直径,与⊙O相切于点,交⊙O于点.已知,则等于度.ODBCA图1CABQPOOPQBAC图2CNM图3ABQO三.最近五年株洲中考有关圆的证明题:1、(本题满分8分)如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆上运动(包含P、Q两点),以线段AB为边向上作等边三角形ABC,(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1)(2)设∠AOB=α,当线段AB与圆O只有一个公共点(即A点)时,求α的范围(如图2,直接写出答案)(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(如图3)2.(2013•株洲)已知AB是⊙O的直径,直线BC与⊙O相切于点B,∠ABC的平分线BD交⊙O于点D,AD的延长线交BC于点C.(1)求∠BAC的度数;(2)求证:AD=CD.3.(2012•株洲)如图,已知AD为⊙O的直径,B为AD延长线上一点,BC与⊙O切于C点,∠A=30°.求证:(1)BD=CD;(2)△AOC≌△CDB.考点:切线的性质;全等三角形的判定;圆周角定理。解答:证明:(1)∵AD为⊙O的直径,∴∠ACD=90°,又∵∠A=30°,OA=OC=OD,∴∠ACO=30°,∠ODC=∠OCD=60°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)又∵BC与⊙o切于C,∴∠OCB=90°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)∴∠BCD=30°,∴∠B=30°,∴∠BCD=∠B,∴BD=CD.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2)∵∠A=∠ACO=∠BCD=∠B=30°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)∴AC=BC,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)在△AOC和△BDC中,∴△AOC≌△BDC(ASA).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)点评:此题考查了切线的性质、等腰三角形的判定与性质以及全等三角形的判定.此题难度适中,注意数形结合思想的应用.4.(2011株洲)(8分)如图,为⊙O的直径,为⊙O的切线,交⊙O于点,为上一点,.(1)求证:;(2)若,,求的长.(1)证明:是⊙O的切线,为⊙O的直径,……2分OEDCBAPEOABC又……3分……4分(2)解:,为圆心为中点……6分又……8分5.(2010年株洲)(8分)如图,是⊙O的直径,为圆周上一点,,⊙O过点的切线与的延长线交于点.求证:(1);(2)≌.证明:(1)∵是⊙O的直径,∴,由,∴又,∴∴,∴.……4分(2)在中,,得,又,∴.由切⊙O于点,得.在和中,∴≌……8分6.(2009年株洲)(10分)如图,点、、是⊙O上的三点,.(1)求证:平分.(2)过点作于点,交于点.若,,求的长.证明:(1)∵,∴;∵,∴∴即平分.…………5分DCBOA解:(2)∵∴又,∴∴,∴,设,则,根据勾股定理得,解得(或者用)即的长是.………………………10分7、(2008年株洲)(7分)如图所示,⊙O的直径AB=4,点P是AB延长线上的一点,过点P作⊙O的切线,切点为C,连结AC.(1)若∠CPA=30°,求PC的长;(2)若点P在AB的延长线上运动,∠CPA的平分线交AC于点M.你认为∠CMP的大小是否发生变化?若变化,请说明理由;若不变化,请求出∠CMP的值.POBACM