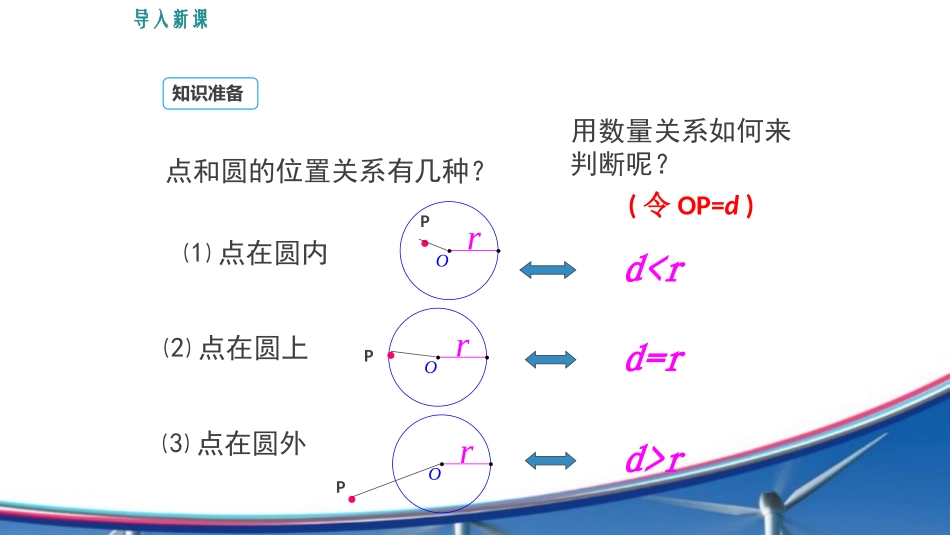
24.2.2直线和圆的位置关系第1课时直线和圆的位置关系导入新课讲授新课当堂练习课堂小结1.了解直线和圆的位置关系.2.了解直线与圆的不同位置关系时的有关概念.3.理解直线和圆的三种位置关系时圆心到直线的距离d和圆的半径r之间的数量关系.(重点)4.会运用直线和圆的三种位置关系的性质与判定进行有关计算.(难点)学习目标点和圆的位置关系有几种?dr用数量关系如何来判断呢?⑴点在圆内rO·P⑵点在圆上rO·P⑶点在圆外rO·P(令OP=d)导入新课知识准备导入新课情境引入问题1如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?讲授新课直线与圆的位置关系的定义一问题2请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?●●●l02直线与圆的位置关系图形公共点个数公共点名称直线名称2个交点割线1个切点切线0个相离相切相交位置关系公共点个数填一填:问题3根据上面观察的发现结果,你认为直线与圆的位置关系可以分为几类?你分类的依据是什么?分别把它们的图形在草稿纸上画出来.①直线与圆最多有两个公共点.②若直线与圆相交,则直线上的点都在圆上.③若A是⊙O上一点,则直线AB与⊙O相切.④若C为⊙O外一点,则过点C的直线与⊙O相交或相离.⑤直线a和⊙O有公共点,则直线a与⊙O相交.判一判:√××××1.已知圆的半径为6cm,设直线和圆心的距离为d:(3)若d=8cm,则直线与圆______,直线与圆有____个公共点.(2)若d=6cm,则直线与圆______,直线与圆有____个公共点.(1)若d=4cm,则直线与圆,直线与圆有____个公共点.(3)若AB和⊙O相交,则.2.已知⊙O的半径为5cm,圆心O与直线AB的距离为d,根据条件填写d的范围:(1)若AB和⊙O相离,则;(2)若AB和⊙O相切,则;相交相切相离d>5cmd=5cm0cm≤d<5cm210练一练:问题1刚才同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?相关知识:点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.lAO直线与圆的位置关系的性质与判定二问题2怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?Od合作探究直线和圆相交drrd∟rd∟rd数形结合:位置关系数量关系(用圆心O到直线的距离d与圆的半径r的关系来区分)ooo性质判定直线与圆的位置关系的性质与判定的区别:位置关系数量关系.公共点个数典例精析BCA43例在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?(1)r=2cm;(2)r=2.4cm;(3)r=3cm.分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.D解:过C作CD⊥AB,垂足为D.在△ABC中,AB=22ACBC22345.根据三角形的面积公式有11.22CDABACBC∴342.4(cm),5ACBCCDAB即圆心C到AB的距离d=2.4cm.所以(1)当r=2cm时,有d>r,因此⊙C和AB相离.BCA43Dd记住:斜边上的高等于两直角边的乘积除以斜边.(2)当r=2.4cm时,有d=r.因此⊙C和AB相切.BCA43Dd(3)当r=3cm时,有d