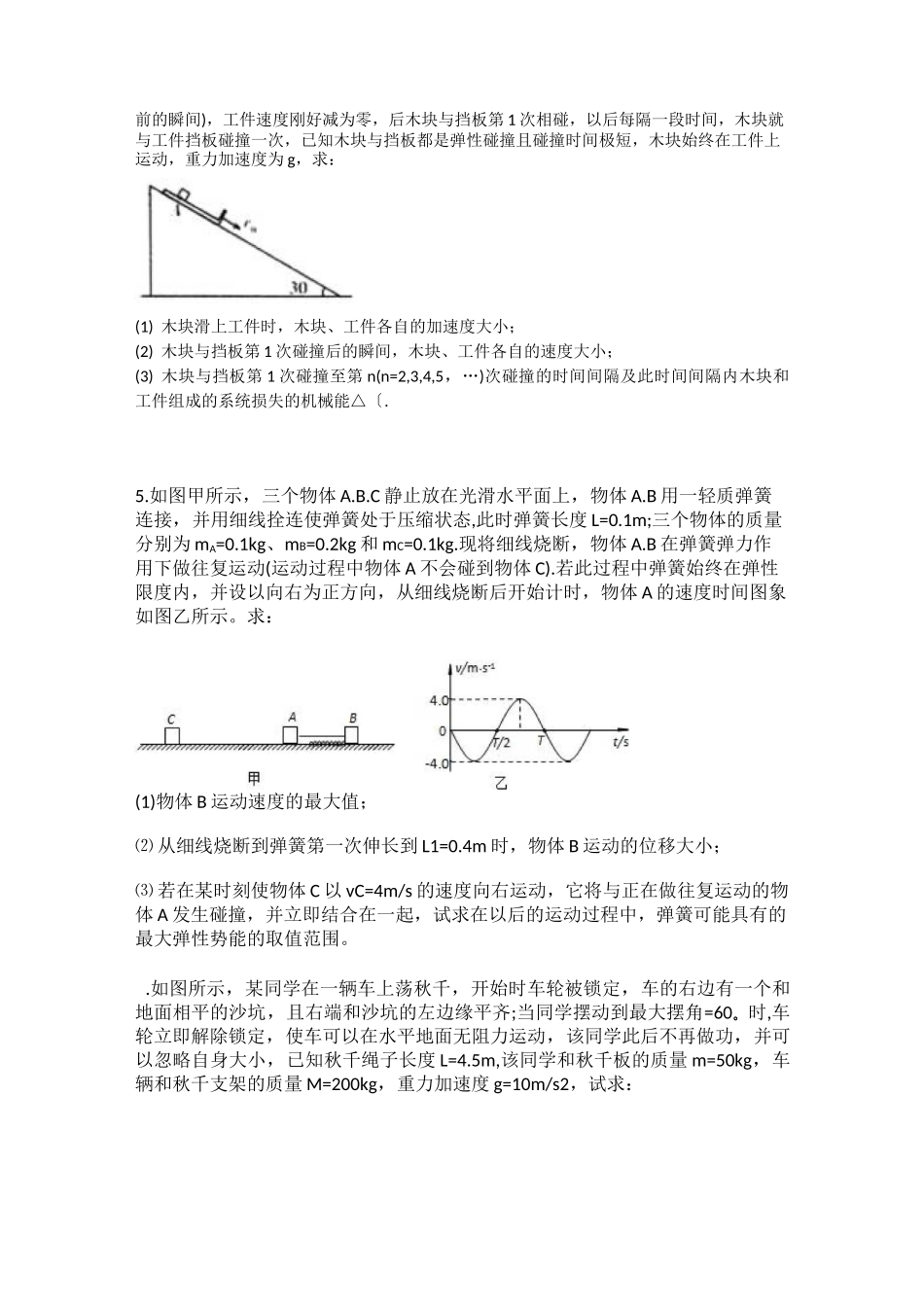
一.力学综合压轴题如图所示,为竖直平面内的光滑绝缘轨道,直轨道和圆弧轨道相切于点,圆弧轨道半径为,与水平面的夹角为e=53°,为圆弧轨道的竖直直径,整个轨道处于竖直向下的匀强电场中。带正电的小球质量为,带电荷量为电荷量始终不变,若将小球从点由静止释放,则它运动到轨道最低点时对轨道的压力大小为3.6为重力加速度。现让一不带电的质量为的绝缘小球从直轨道的点由静止释放,运动到点时恰好与静止在点的小球发生弹性碰撞。不计空气阻力,53°=0.,53°=0.6。求匀强电场的电场强度的大小若二,且碰后小球恰好到达最高点,则轨道点离点的高度为多少3若在点碰撞后小球的速度大小为于,,则小球从点离开轨道到再次回到轨道的时间为多长一置于竖直平面内、倾匍=3。的光滑斜面的顶端连结一光滑的半径为圆心角为。的圆弧轨道圆弧轨道与斜面相切于点一轻质弹簧的下端与光滑斜面底端的固定挡板连接上端与小球接触不连接静止在点。在点由静止释放一小滑块滑块在点与小球相碰碰后瞬间小球嵌入滑块形成一个组合体。组合体沿着斜面上升到的中点时速度为零。已知小球和滑块质量均为之间的距离为重力加速度为。=3.6°=0..计算结果可含根式求碰撞后瞬间,组合体的速度大小;求碰撞前弹簧的弹性势能;若在点给滑块一个沿斜面向下的初速度滑块与小球相碰后组合体沿斜面上滑进入圆弧轨道从轨道最高点离开后做平抛运动当运动到与圆心等高时组合体与点的距离为求初速度的大小。如图所示为放置在竖直平面内游戏滑轨的模拟装置滑轨由四部分粗细均匀的金属杆组成其中倾斜直轨与水平直轨长均为圆弧形轨道和均光滑、与两圆弧形轨道相切的半径为的半径为、与竖直方向的夹角均为0。现有一质量为的小球穿在滑轨上以的初动能从点开始沿向上运动小球与两段直轨道间的动摩擦因数均为M设小球经过轨道连接处均无能量损失。。求:要使小球能够通过弧形轨道的最高点初动能至少多大求小球第二次到达点时的动能;小球在段上运动的总路程第两问中的取第问中的数值如图所示,固定斜面足够长,斜面与水平面的夹角a=30。,一质量为3m的“L”型工件沿斜面以速度v0匀速向下运动,工件上表面光滑,下端为挡板。某时,一质量为m的小木块从工件上的A点,沿斜面向下以速度v°滑上工件,当木块运动到工件下端时(与挡板碰前的瞬间),工件速度刚好减为零,后木块与挡板第1次相碰,以后每隔一段时间,木块就与工件挡板碰撞一次,已知木块与挡板都是弹性碰撞且碰撞时间极短,木块始终在工件上运动,重力加速度为g,求:(1)木块滑上工件时,木块、工件各自的加速度大小;(2)木块与挡板第1次碰撞后的瞬间,木块、工件各自的速度大小;(3)木块与挡板第1次碰撞至第n(n=2,3,4,5,…)次碰撞的时间间隔及此时间间隔内木块和工件组成的系统损失的机械能△〔.5.如图甲所示,三个物体A.B.C静止放在光滑水平面上,物体A.B用一轻质弹簧连接,并用细线拴连使弹簧处于压缩状态,此时弹簧长度L=0.1m;三个物体的质量分别为mA=0.1kg、mB=0.2kg和mC=0.1kg.现将细线烧断,物体A.B在弹簧弹力作用下做往复运动(运动过程中物体A不会碰到物体C).若此过程中弹簧始终在弹性限度内,并设以向右为正方向,从细线烧断后开始计时,物体A的速度时间图象如图乙所示。求:(1)物体B运动速度的最大值;⑵从细线烧断到弹簧第一次伸长到L1=0.4m时,物体B运动的位移大小;⑶若在某时刻使物体C以vC=4m/s的速度向右运动,它将与正在做往复运动的物体A发生碰撞,并立即结合在一起,试求在以后的运动过程中,弹簧可能具有的最大弹性势能的取值范围。.如图所示,某同学在一辆车上荡秋千,开始时车轮被锁定,车的右边有一个和地面相平的沙坑,且右端和沙坑的左边缘平齐;当同学摆动到最大摆角=60。时,车轮立即解除锁定,使车可以在水平地面无阻力运动,该同学此后不再做功,并可以忽略自身大小,已知秋千绳子长度L=4.5m,该同学和秋千板的质量m=50kg,车辆和秋千支架的质量M=200kg,重力加速度g=10m/s2,试求:⑴该同学摆到最低点时的速率;⑵在摆到最低点的过程中,绳子对该同学做的功;⑶该同学到最低点时,顺势离开秋千板,他落入沙坑的位置距离左边界多远?已知车辆长度s=3.6m...