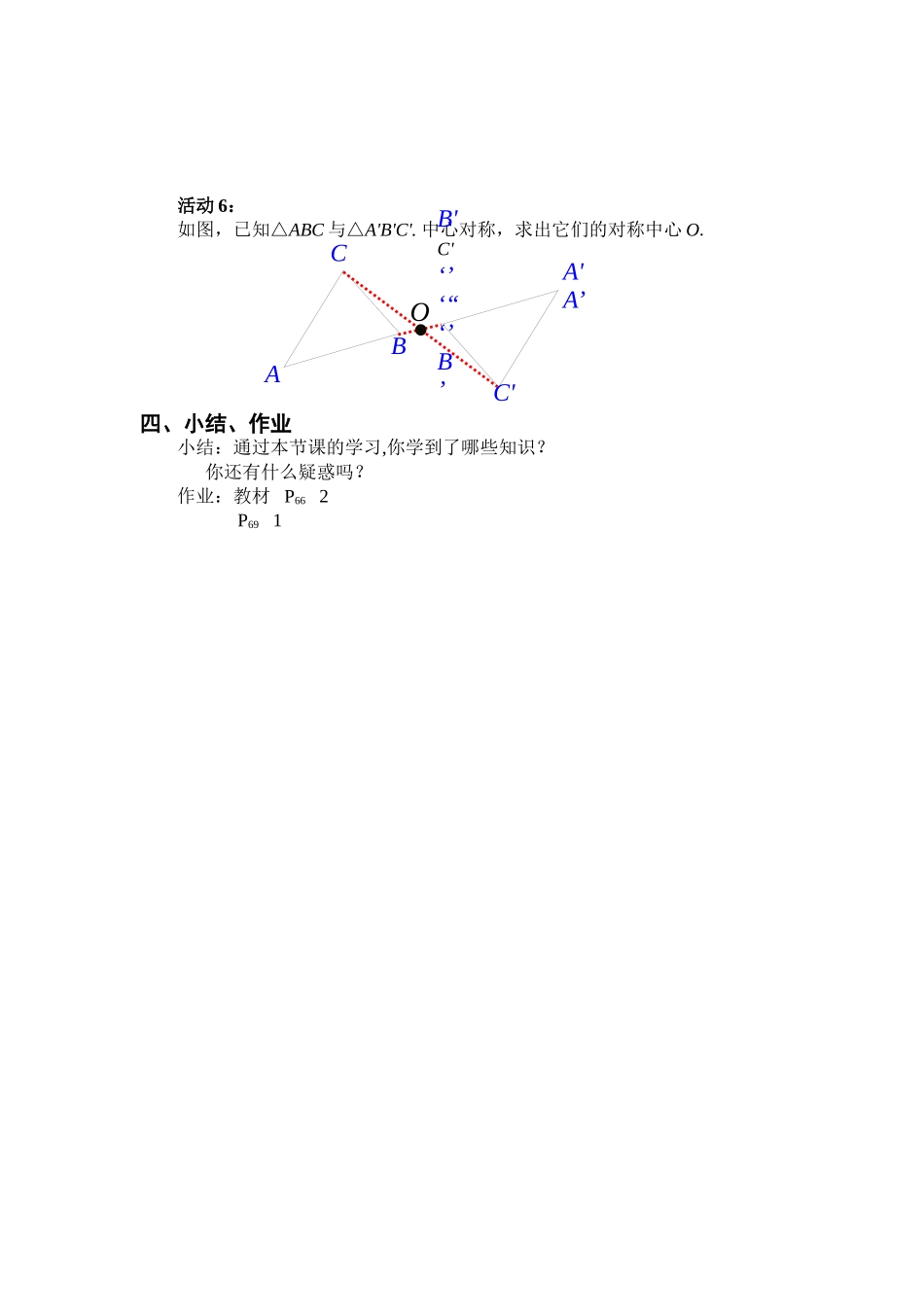
三、教学过程活动1:欣赏下面4个图形,回答问题:(1)这4个图形绕着各自的中心点旋转多少度后,能与自身重合?(2)以上4个图形绕中心点旋转180°,哪些会与自身重合?(教师提出问题,学生观察思考并回答)活动2:观察一:(1)如图,把其中一个图案绕点O旋转180°你有什么发现?观察二:(2)如图,线段AC,BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你有什么发现?(两个图形能够重合,总结共同的规律,绕某一点旋转180°,能与另一个图形重合,导出中心对称的概念)中心对称:把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.△OCD和△OAB关于点O对称,点C与点A是关于点O的对称点.活动3:如图,旋转三角板,画关于点O对称的两个三角形:OABDCO(1)(2)(3)ABDCO第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出△A′B′C′;第三步,移开三角板.这样画出的△ABC和△A′B′C′关于点O对称。分别连接AA′,BB′,CC′.点O在线段AA′上吗?如果在,在什么位置?△ABC与△A′B′C′有什么关系?让学生发现:(1)点O是线段AA′的中点;(2)△ABC≌△A′B′C′归纳性质:(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.(2)关于中心对称的两个图形是全等图形.巩固性质:如图,△ABD与△CDB关于BD的中点O成中心对称,下列说法,不正确的是()A.AD=BCB.ADBCC.连接AC,则AO=OCD.△OAD与△OCD全等活动4:[例1](1)如图,选择点O为对称中心,画出点A关于点O的对称点A′.(2)如图,选择点O为对称中心,画出△ABC关于点O的对称的△A'B'C'.析:(1)画法:连接AO并延长到A′,使OA′=OA,得到点A的对称点A′.(2)连接AO并延长到A′,使OA′=OA,得到点A的对称点A′;同样画B、C的对称点B′、C′;△A′B′C′即为所求的三角形.活动5:变式训练:如图,选择点O为对称中心,画出△ABC关于点O的对称的△A'B'C'.(1)(2)OABDCOABDCBACOBACOBACOBACOBACO活动6:如图,已知△ABC与△A'B'C'.中心对称,求出它们的对称中心O.四、小结、作业小结:通过本节课的学习,你学到了哪些知识?你还有什么疑惑吗?作业:教材P662P691OABCA'A’B'C'‘’‘“‘’B’C'