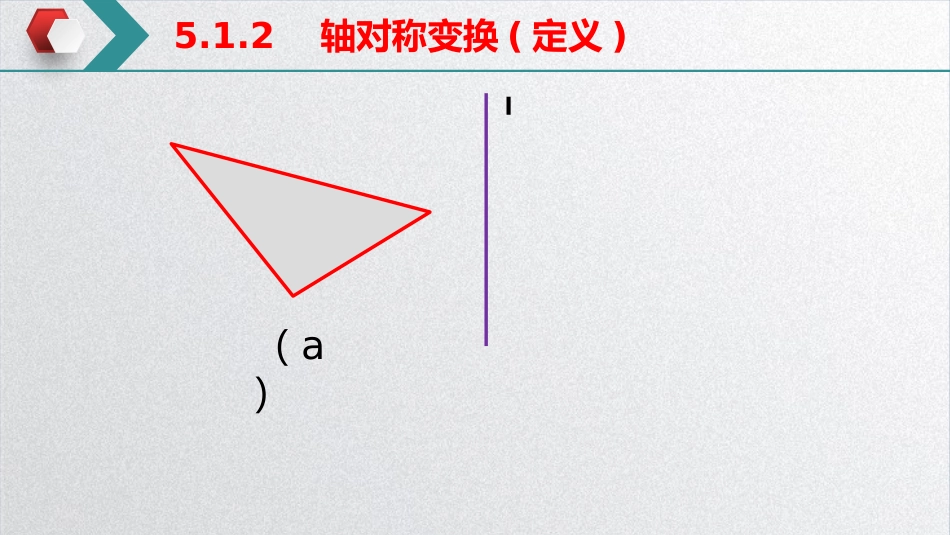
湘教版数学七年级下册临澧县丁玲学校谭金梅5.1.25.1.2轴对称变换(定义)(a)l5.1.2轴对称变换(定义)把图形(a)沿着直线l翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l作了轴对称变换,也叫轴反射.(b)(a)l5.1.2轴对称变换(定义)原像像l一个图形关于某一条直线作轴对称变换后,能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也称这两个图形成轴对称.5.1.2轴对称变换(定义)(b)(a)l三角形(a)和三角形(b)成轴对称.对称轴5.1.2轴对称变换(定义)(b)对应点AAˊ(a)三角形(a)和三角形(b)关于直线l对称.5.1.2轴对称变换(定义)5.1.2轴对称变换两个图形成轴对称轴对称图形两个图形成轴对称和轴对称图形的联系和区别5.1.2轴对称变换(定义)两个图形成轴对称和轴对称图形的联系和区别两个图形成轴对称轴对称图形图形(示例)区别图形个数对应点对称轴联系两个图形一个图形对应点在两个图形上对应点在一个图形上一条一条或多条或无数条沿着一条直线对折后,直线两侧的部分都能重合5.1.2轴对称变换(定义)5.1.2轴对称变换下列两幅图中,哪个是轴对称图形?哪个是成轴对称?②2⑥6⑤5练习①下列左右两个图形成轴对称的有()组.④4③325.1.2轴对称变换5.1.2轴对称变换(性质)活动目标:探究轴对称变换的性质活动方式:小组合作活动准备:学具、直尺、量角器活动过程:1.画一画在半透明纸上分别画出:(1)点P关于直线l的对应点P′,连接PP′与l交于点O.(2)线段EF关于直线l对应线段E′F′,分别连接EE′,FF′,与l交于点M、N.(3)三角形ABC关于直线l的对称图形三角形A′B′C′,连接AA′,与l交于点E.2.量一量(精确到0.1cm)①OP=_____cmOP′=_____cm②ME=_____cmME′=_____cmNF=_____cmNF′=_____cm③AE=_____cmA′E=_____cm3.比一比①OP_____OP′②ME_____ME′NF_____NF′③AE_____A′E我发现:对应点的连线被对称轴________.4.量一量各组对应点与对称轴相交时所形成的角的度数,我发现:每个角都是_____,我认为:对应点的连线与对称轴___________.5.结论:轴对称变换________图形的_______和_______.成轴对称的两个图形中,对应点的连线被对称轴_________.⑴lPlEFACBl⑵⑶探究5.1.2轴对称变换(性质)lPP'OlEE'NFF'MACBB'A'C'lE轴对称变换不改变图形的形状和大小.(4)三角形ABC的周长是__________,三角形AˊBˊCˊ的面积是____________.如图,三角形ABC与三角形AˊBˊCˊ关于直线l对称,且AB=4cm,BˊCˊ=3cm,AC=5cm,∠Bˊ=90°,∠A=37°,则练习B'ACBA'C'(1)点A的对应点是_________,点Bˊ的对应点是_________,点C的对应点是_________.(2)AB=________,BC=________ˊˊ,AC=________ˊˊ(3)∠C=________°4cm点B点A'3cm5cm5312cml6点C'5.1.2轴对称变换(性质)图形经过轴对称变换,长度、角度和面积等都不改变.探究5.1.2轴对称变换(性质)lPP'OlEE'NFF'MACBB'A'C'lE成轴对称的两个图形中,对应点的连线被对称轴垂直平分.探究5.1.2轴对称变换(性质)B'ACBA'C'PDl2E1··P'因为沿l对折,点P和点Pˊ重合,所以PD与PˊD,∠1与∠2也互相重合,所以PD=PˊD,∠1=∠2.又因为∠1+∠2=180°,所以∠1=∠2=90°.所以PPˊ被l垂直平分.①轴对称变换不改变图形的形状和大小.②成轴对称的两个图形中,对应点的连线被对称轴垂直平分.轴对称变换的性质:几何语言:因为∠1=∠2=90°,PD=PD'所以l┴PP',l平分PP'探究5.1.2轴对称变换(性质)B'lACA'C'PD2E1·P'·B5.1.2轴对称变换(应用)5.1.2轴对称变换(应用)11、3、2、轴对称变换后的像原来的图形猜一猜英语单词5.1.2轴对称变换(应用)5.1.2轴对称变换(应用)5.1.2轴对称变换(应用)12我是大诗人:下列三句话具有对称规律,你能把它们补充完整吗?5.1.2轴对称变换(应用)①上海自来水()②清水池里()③山西悬空寺()来自海上池水清空悬西山5.1.2轴对称变换(应用)5.1.2轴对称变换(应用)123一次晚会上,主持人出了一道题目:“如何把变成一个真正的等式?”过了很长时间,也没有人答出,小兰很快解决了这道题目。你知道她是怎样做的吗?5.1.2轴对称变换(应用)5.1.2轴对...