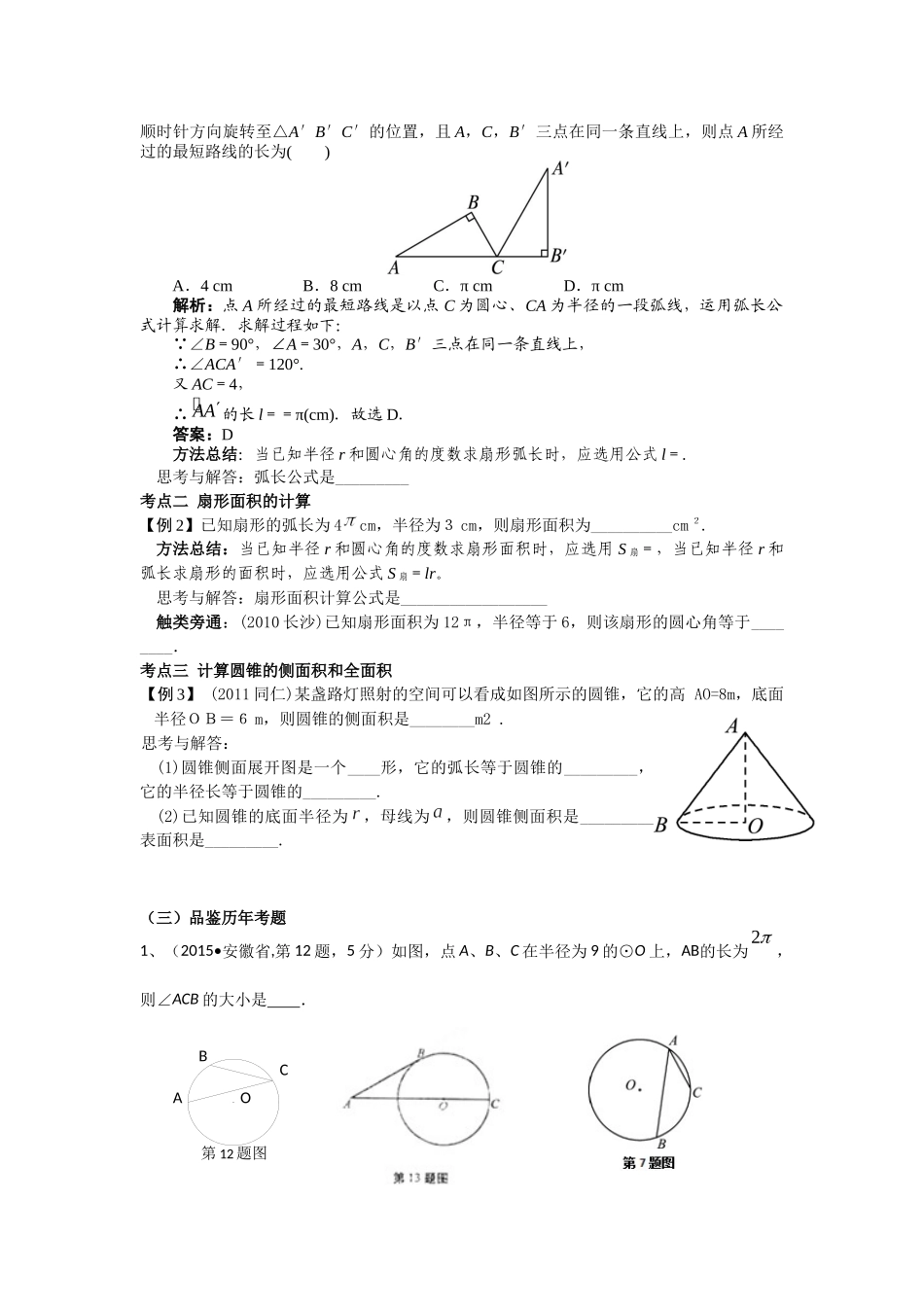
《与圆有关的计算》复习课教学设计一、知识内容分析本节课是基于沪科版教材九年级下册的《与圆有关的计算》专题复习课。由于圆本身所具有的数学美、趣味、规则、对称等特点,使得研究圆可以系统、规范、严谨地培养学生的数学思维。本节课运用弧长、扇形面积、圆锥侧面积与圆的关系解决实际问题。同时通过本专题的学习,提高学生观察图形、分析、归纳整理信息以及应用转化的数学思想方法解决问题的能力,为后续的深入复习与提高打下良好的基础。二、学情诊断分析初三学生经过将近三年的学习有一定的数学基础,但是学习层次各有不同大致可分为以下三个层次:1.能通过观察发现图形所具有的特点,并能大概判断解题方向,但对计算公式不熟悉;2.熟悉计算公式,但不知道在什么样的条件下用什么公式和方法将知识综合运用;3.对计算公式熟练,并掌握一定数学思想方法,在解题过程中能较为自如地运用。由于学生的学习层次不一样,基础差的学生在得不到小组或者教师的支持时可能会放弃学习和讨论,因此教师要充分关注基础差的学生的学习状态,及时给予帮助和指导。三、教学目标(一)知识与技能:1.掌握弧长和扇形面积公式,会计算圆的弧长和扇形面积.2.了解圆锥侧面展开图为一个扇形,会计算圆锥的侧面积和全面积.(二)过程与方法:1.让学生通过习题训练,加深对弧长公式和扇形面积公式的理解。2.在探索弧长、扇形面积、圆锥的侧面积和全面积有关计算的过程中,体会转化思想、类比迁移思想在解决问题中的重要性。(三)情感、态度与价值观:通过本专题的学习,培养学生自主探究与合作交流的能力,收获解题的成功感,并受到数学图形美的熏陶.四、教学重难点:重点:1.圆的弧长和扇形面积的计算;2.掌握圆锥侧面积与全面积的计算难点:有关弧长和扇形面积的综合应用.五、教学方法:通过大量的中考模拟题,采用启发式教学,从学生原有知识出发,充分发挥学生的主体作用。同时注重知识间的联系,类比迁移。六、教学手段:采用多媒体辅助教学,使有限的时间成为无限的空间,促进学生自主学习。事先教师准备好习题纸、电脑、课件等;学生事先复习相关知识,准备直尺、三角板、圆规等。七、教学过程(一)考点知识解读和梳理与圆有关的计算命题解读近7年中考对弧长的计算共考查了4次,预计2017年中考仍将考查弧长的计算,且较为基本;扇形的面积计算也不能放松;常以选择题、填空题的形式出现。考查知识扇形的弧长公式扇形弧长为l,圆心角的度数为n°,圆的半径为rl=扇形的面积公式S扇=,S扇=lr(二)考点方法探究考点一弧长的有关计算【例1】如图,在△ABC中,∠B=90°,∠A=30°,AC=4cm,将△ABC绕顶点CAOCB第12题图顺时针方向旋转至△A′B′C′的位置,且A,C,B′三点在同一条直线上,则点A所经过的最短路线的长为()A.4cmB.8cmC.πcmD.πcm解析:点A所经过的最短路线是以点C为圆心、CA为半径的一段弧线,运用弧长公式计算求解.求解过程如下: ∠B=90°,∠A=30°,A,C,B′三点在同一条直线上,∴∠ACA′=120°.又AC=4,∴的长l==π(cm).故选D.答案:D方法总结:当已知半径r和圆心角的度数求扇形弧长时,应选用公式l=.思考与解答:弧长公式是_________考点二扇形面积的计算【例2】已知扇形的弧长为4cm,半径为3cm,则扇形面积为__________cm2.方法总结:当已知半径r和圆心角的度数求扇形面积时,应选用S扇=,当已知半径r和弧长求扇形的面积时,应选用公式S扇=lr。思考与解答:扇形面积计算公式是__________________触类旁通:(2010长沙)已知扇形面积为12π,半径等于6,则该扇形的圆心角等于________.考点三计算圆锥的侧面积和全面积【例3】(2011同仁)某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8m,底面半径OB=6m,则圆锥的侧面积是________m2.思考与解答:(1)圆锥侧面展开图是一个____形,它的弧长等于圆锥的_________,它的半径长等于圆锥的_________.(2)已知圆锥的底面半径为,母线为,则圆锥侧面积是_________,表面积是_________.(三)品鉴历年考题1、(2015•安徽省,第12题,5分)如图,点A、B、C在半径为9的⊙O上,AB的长为,则∠ACB的大...