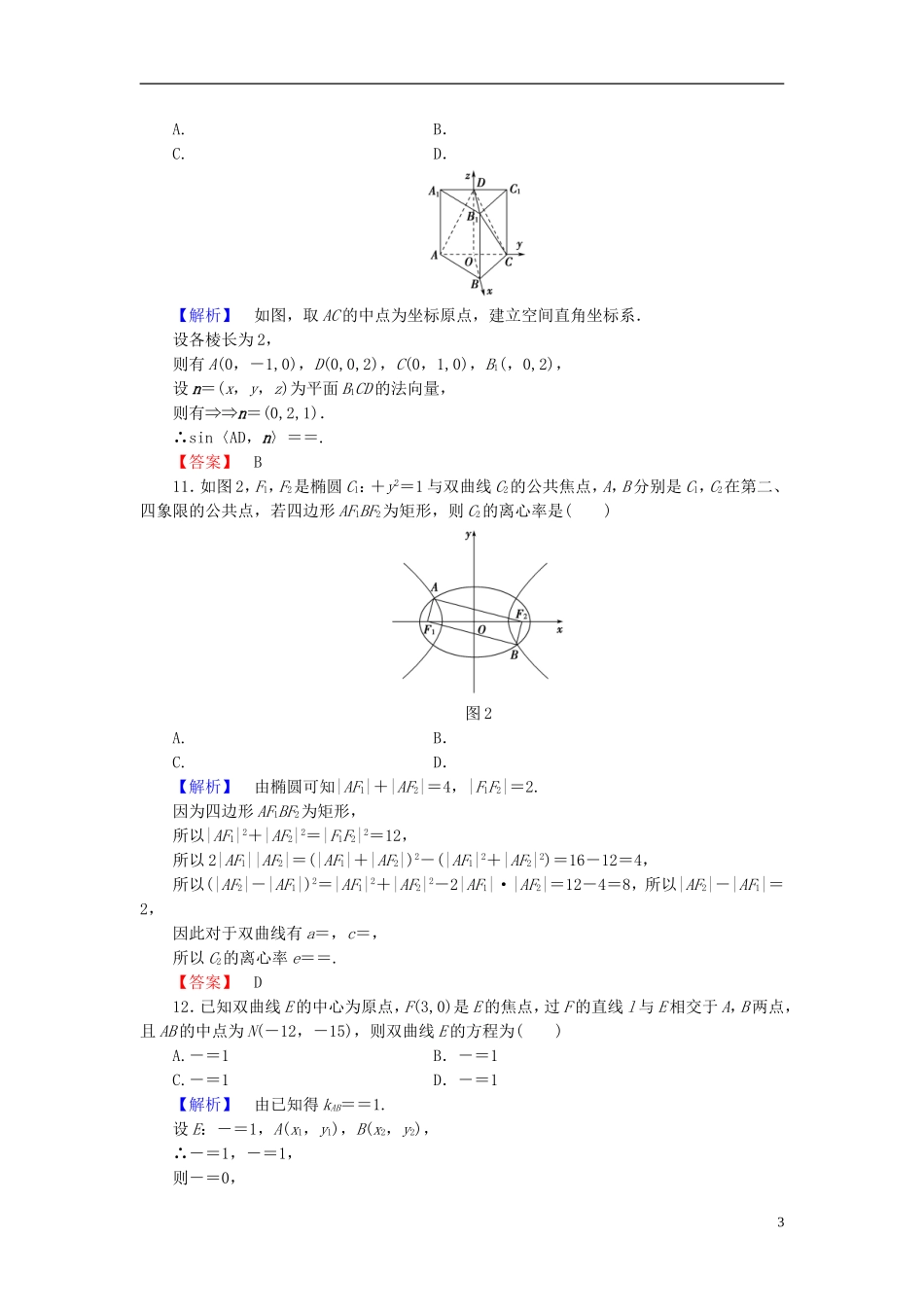
模块综合测评(一)(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.命题“若p则q”的逆命题是()A.若q则pB.若綈p则綈qC.若綈q则綈pD.若p则綈q【解析】根据原命题与逆命题之间的关系可得:逆命题为“若q则p”,选A.【答案】A2.已知命题p:在直角坐标平面内,点M(sinα,cosα)与N(1,2)在直线x+y-2=0的异侧;命题q:若向量a,b满足a·b>0,则向量a,b的夹角为锐角.以下命题中为真命题的是()A.p或q真,p且q真B.p或q真,p且q假C.p或q假,p且q真D.p或q假,p且q假【解析】 sinα+cosα-2≤-2<0,∴点M(sinα,cosα)在直线x+y-2=0的左下侧.又 1+2-2>0,∴N(1,2)在直线x+y-2=0的右上侧,故命题p为真.若向量a,b满足a·b>0,则向量a,b的夹角为锐角,显然为假.因为当a,b同向时,设a·b=1>0,但是a,b夹角为0,所以命题q为假.【答案】B3.设p:x<-1或x>1,q:x<-2或x>1,则綈p是綈q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】綈p:-1≤x≤1;綈q:-2≤x≤1,显然{x|-1≤x≤1}{x|-2≤x≤1},所以綈p是綈q的充分不必要条件.【答案】A4.已知抛物线顶点在坐标原点,焦点在y轴上,抛物线上的点M(m,-2)到焦点的距离为4,则m等于()A.4B.2C.4或-4D.2或-2【解析】由已知可设抛物线方程为x2=-2py(p>0),由抛物线的定义知2+=4,∴p=4.∴x2=-8y.将(m,-2)代入上式得m2=16,∴m=±4.【答案】C5.已知E、F分别是正方体ABCDA1B1C1D1中BB1、DC的中点,则异面直线AE与D1F所成的角为()A.30°B.60°C.45°D.90°【解析】以A1为原点,A1B1、A1D1、A1A为x轴、y轴、z轴建立空间直角坐标系.不妨设正方体的棱长为2,则A(0,0,2),E(2,0,1),D1(0,2,0),F(1,2,2),AE=(2,0,-1),D1F=(1,0,2),所以AE·D1F=0,所以AE⊥D1F,即AE与D1F所成的角为90°.【答案】D6.抛物线y2=4x的焦点到双曲线x2-=1的渐近线的距离是()1【导学号:32550101】A.B.C.1D.【解析】由题意可得,抛物线的焦点为(1,0),双曲线的渐近线方程为y=±x,即±x-y=0,由点到直线的距离公式可得抛物线的焦点到双曲线的渐近线的距离d==.【答案】B7.如图1所示,空间四边形OABC中,OA=a,OB=b,OC=c,点M在OA上,且OM=2MA,点N为BC的中点,则MN等于()图1A.a-b+cB.-a+b+cC.a+b-cD.-a+b-c【解析】连接ON,由向量加法法则,可知MN=MO+ON=-OA+(OB+OC)=-a+(b+c)=-a+b+c.故选B.【答案】B8.已知椭圆+=1(a>b>0),M为椭圆上一动点,F1为椭圆的左焦点,则线段MF1的中点P的轨迹是()A.椭圆B.圆C.双曲线的一支D.线段【解析】 P为MF1中点,O为F1F2的中点,∴|OP|=|MF2|,又|MF1|+|MF2|=2a,∴|PF1|+|PO|=|MF1|+|MF2|=a.∴P的轨迹是以F1,O为焦点的椭圆.【答案】A9.若双曲线的实轴长与虚轴长之和等于其焦距的倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为()A.-=1B.-=1C.-=1D.-=1【解析】由于双曲线的顶点坐标为(0,2),可知a=2,∴双曲线的标准方程为-=1.根据题意,得2a+2b=×2c,即a+b=c.又 a2+b2=c2,且a=2,解得b2=4,∴适合题意的双曲线方程为-=1,故选B.【答案】B10.正三棱柱ABCA1B1C1的所有棱长都相等,D是A1C1的中点,则直线AD与平面B1DC所成角的正弦值为()2A.B.C.D.【解析】如图,取AC的中点为坐标原点,建立空间直角坐标系.设各棱长为2,则有A(0,-1,0),D(0,0,2),C(0,1,0),B1(,0,2),设n=(x,y,z)为平面B1CD的法向量,则有⇒⇒n=(0,2,1).∴sin〈AD,n〉==.【答案】B11.如图2,F1,F2是椭圆C1:+y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是()图2A.B.C.D.【解析】由椭圆可知|AF1|+|AF2|=4,|F1F2|=2.因为四边形AF1BF2为矩形,所以|AF1|2+|AF2|2=|F1F2|2=12,所以2|AF1||AF2|=(|AF1|+|AF2|)2-(|AF1|2+|AF2|2)=16-12=4,所以(|AF2|-|AF1|)2=|AF1|2+|AF2|2-2|AF1...