2013届高考物理考纲专项复习-圆周运动课件VIP免费

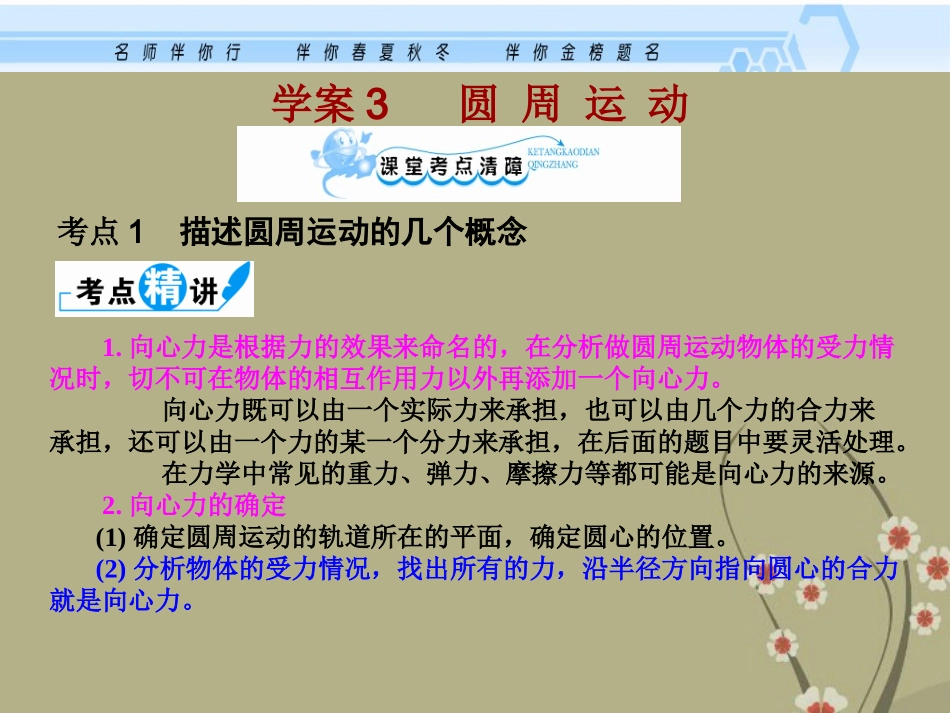
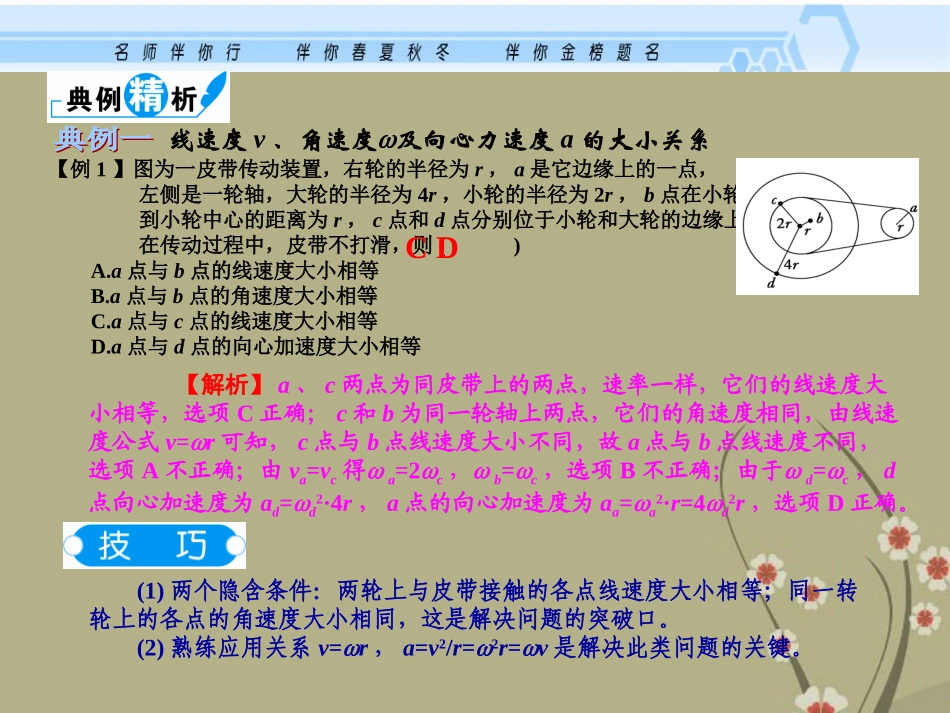
考点1描述圆周运动的几个概念学案3圆周运动1.向心力是根据力的效果来命名的，在分析做圆周运动物体的受力情况时，切不可在物体的相互作用力以外再添加一个向心力。向心力既可以由一个实际力来承担，也可以由几个力的合力来承担，还可以由一个力的某一个分力来承担，在后面的题目中要灵活处理。在力学中常见的重力、弹力、摩擦力等都可能是向心力的来源。2.向心力的确定(1)确定圆周运动的轨道所在的平面，确定圆心的位置。(2)分析物体的受力情况，找出所有的力，沿半径方向指向圆心的合力就是向心力。1.线速度、角速度、周期和转速都可以描述圆周运动的快慢，但意义不同，线速度描述做圆周运动的物体沿圆周运动的快慢，若比较两物体沿圆周运动的快慢，只看线速度大小即可；而角速度、周期和转速描述做圆周运动的物体绕圆心转动的快慢。由=2/T=2f可知，越大，T越小，f越大，则物体转动得越快，反之越慢。三个物理量知其中一个，另两个也就成为已知量。2.在分析传动装置的各物理量时，要抓住不等量和相等量的关系。同轴转动的各点角速度和转速n相等，而线速度v=r与半径r成正比。在不考虑皮带打滑的情况下，传动皮带与皮带连接的两轮边缘的各点线速度大小相等，而角速度=v/r与半径r成反比。线速度v、角速度及向心力速度a的大小关系【例1】图为一皮带传动装置，右轮的半径为r，a是它边缘上的一点，左侧是一轮轴，大轮的半径为4r，小轮的半径为2r，b点在小轮上，到小轮中心的距离为r，c点和d点分别位于小轮和大轮的边缘上，若在传动过程中，皮带不打滑，则()A.a点与b点的线速度大小相等B.a点与b点的角速度大小相等C.a点与c点的线速度大小相等D.a点与d点的向心加速度大小相等(1)两个隐含条件：两轮上与皮带接触的各点线速度大小相等；同一转轮上的各点的角速度大小相同，这是解决问题的突破口。(2)熟练应用关系v=r，a=v2/r=2r=v是解决此类问题的关键。CD【解析】a、c两点为同皮带上的两点，速率一样，它们的线速度大小相等，选项C正确；c和b为同一轮轴上两点，它们的角速度相同，由线速度公式v=r可知，c点与b点线速度大小不同，故a点与b点线速度不同，选项A不正确；由va=vc得a=2c，b=c，选项B不正确；由于d=c，d点向心加速度为ad=d2·4r，a点的向心加速度为aa=a2·r=4d2r，选项D正确。1如图所示，甲、乙、丙三个轮子依靠摩擦传动，相互之间不打滑，其半径分别为r1、r2、r3。若甲轮的角速度为1，则丙轮的角速度为()A.r11/r3B.r31/r1C.r31/r2D.r11/r2A【例2】如图所示，半径为R的圆板做匀速转动，当半径OB转到某一方向时，在圆板中心正上方高h处，以平行于OB方向水平抛出一小球。要使小球与圆板只碰撞一次，且落点为B，求小球水平抛出时的速度v0及圆板转动的角速度分别是多少？圆周运动具有周期性，因此与圆周运动有关的部分题目的解可能具有周期性。分析该部分题目时要注意考虑周期性，把要求的解回答全面，避免出现漏解。【解析】(1)设小球做平抛运动落到B点的时间为t，则R=v0t①h=(1/2)gt2②由①②解得：恰好落在B点，则平抛运动时间t与周期T的关系是：t=nT(n=1,2,…)③又因为T=2/④由以上各式解得：(n=1,2…)。【答案】(n=1,2...)2gRh2gnh02gvRh2gnh圆周运动的周期性问题【答案】如图所示，直径为d的纸筒，以角速度绕O轴转动，一颗子弹沿直径水平穿过圆纸筒，先后留下a、b两个弹孔，且Oa、Ob间的夹角为，则子弹的速度为多少？(0,1,2,3)(21)dnn2圆周运动的临界问题，往往发生在物体在竖直平面内的变速圆周运动问题中，中学阶段只分析物体通过最高点和最低点的情况。(1)如图所示，是没有物体支撑的小球，在竖直平面内做圆周运动经过最高点的情况。注意：绳对小球只能产生沿绳收缩方向的拉力。①临界条件：当小球恰好能沿圆周通过最高点时，绳子或轨道对小球没有力的作用。mg=mv2/Rv临界=。注意：如果小球带电，且空间存在电、磁场时，临界条件应是小球重力、电场力和洛伦兹力的合力作为向心力，此时临界速度v临界≠。②能过最高点的条件：v≥，当v>时，向心力F向=mv2/R≥mg，则绳对球产生拉...