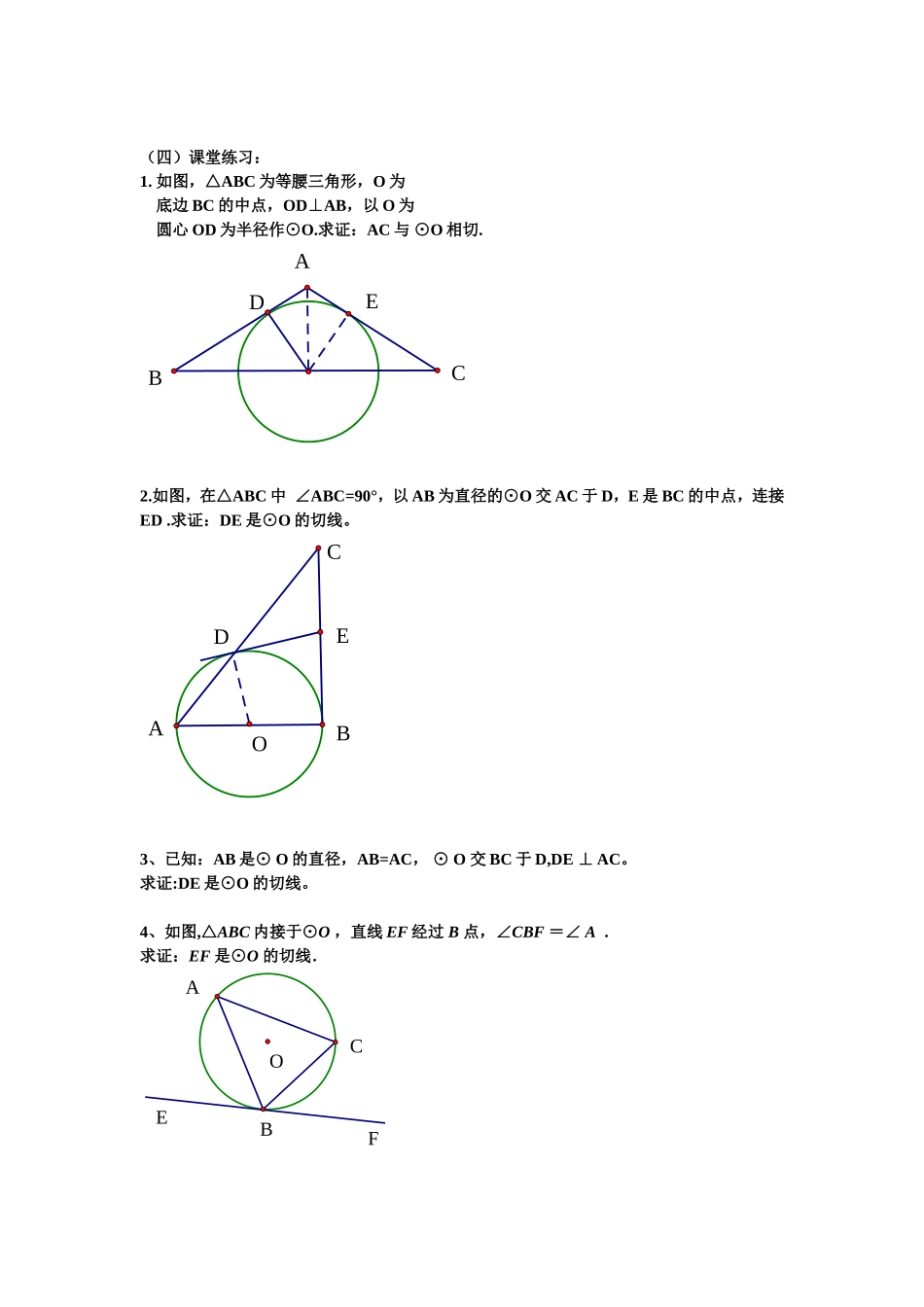
切线的性质和判定教学设计【教学目标】一、知识和技能:1、理解切线的判定定理和性质定理,并会灵活应用。2、结合不同题目的不同已知条件,选择合适的证切线的方法。3、灵活应用切线的判定和性质,解决综合性问题。二、过程和方法:以直线和圆的位置关系为导引,讲述切线的判定的两种方法,并教会学生灵活应用切线的判定和性质。三、情感态度和价值观:让学生感受到实际生活中存在的相切的位置关系,教会学生把实际问题抽象成数学模型。【教学重点】切线的判定定理和性质定理,学会灵活应用,解决问题。【教学难点】根据具体的已知条件选择合适的证切线的方法。【教学方法】自主探索、合作交流。【教学过程】一、新课引入:复习直线和圆的三种位置关系:相离、相切、相交。复习概念:切线、割线、交点、切点。弄清每种情况下d与r的大小关系。二、探究新知:(一)切线的判定:证明一条直线是圆的切线,你有哪些常用方法?方法1:d=r法证明:圆心到直线的距离等于半径常用辅助线:作垂直、证半径方法2:切线的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线。常用辅助线:连半径、证垂直(二)切线的性质:圆的切线垂直于过切点的半径。∵l是⊙O的切线,切点为A∴l⊥OA简记为:“知切线,连半径,得垂直”(三)例题讲解:例1如图,已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。BCAO例2如图,已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。求证:⊙O与AC相切。OCEBDA例3:已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。求证:⊙O与AC相切。(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直.简记为:有交点,连半径,证垂直.(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长.简记为:无交点,作垂直,证半径(四)课堂练习:1.如图,△ABC为等腰三角形,O为底边BC的中点,OD⊥AB,以O为圆心OD为半径作⊙O.求证:AC与⊙O相切.CEBDA2.如图,在△ABC中∠ABC=90°,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED.求证:DE是⊙O的切线。CEDBOA3、已知:AB是⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC。求证:DE是⊙O的切线。4、如图,△ABC内接于⊙O,直线EF经过B点,∠CBF=∠A.求证:EF是⊙O的切线.FEOCBA四、课堂小结:1、判定切线的方法有哪些?2.常用的添辅助线方法?3.圆的切线性质定理:圆的切线垂直于圆的半径。师生行为:让学生尝试归纳,总结,发言,体会、反思。教师点评汇总。设计意图:归纳反思、加强学习反思、帮助学生养成彻底整理知识的习惯。