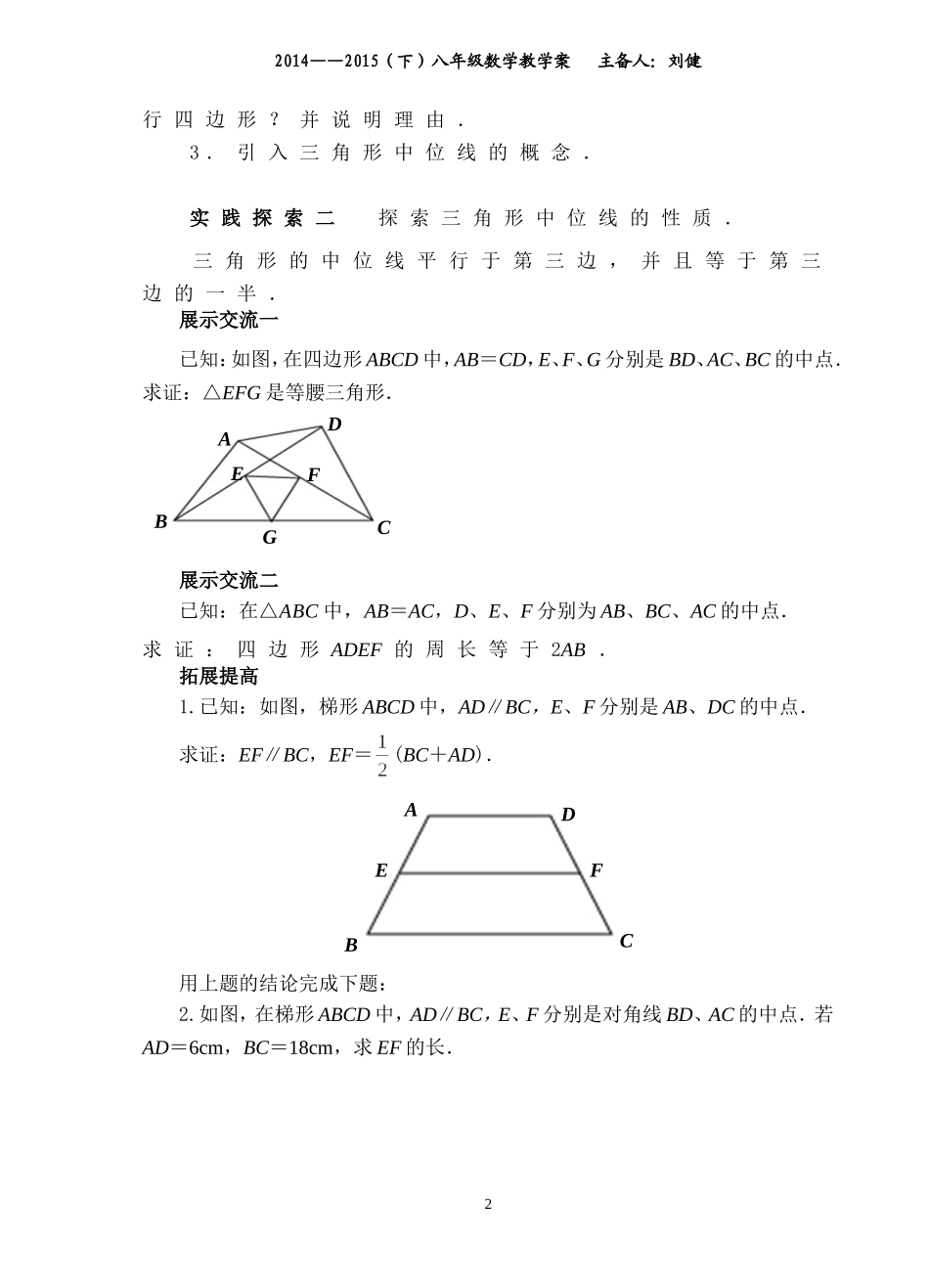
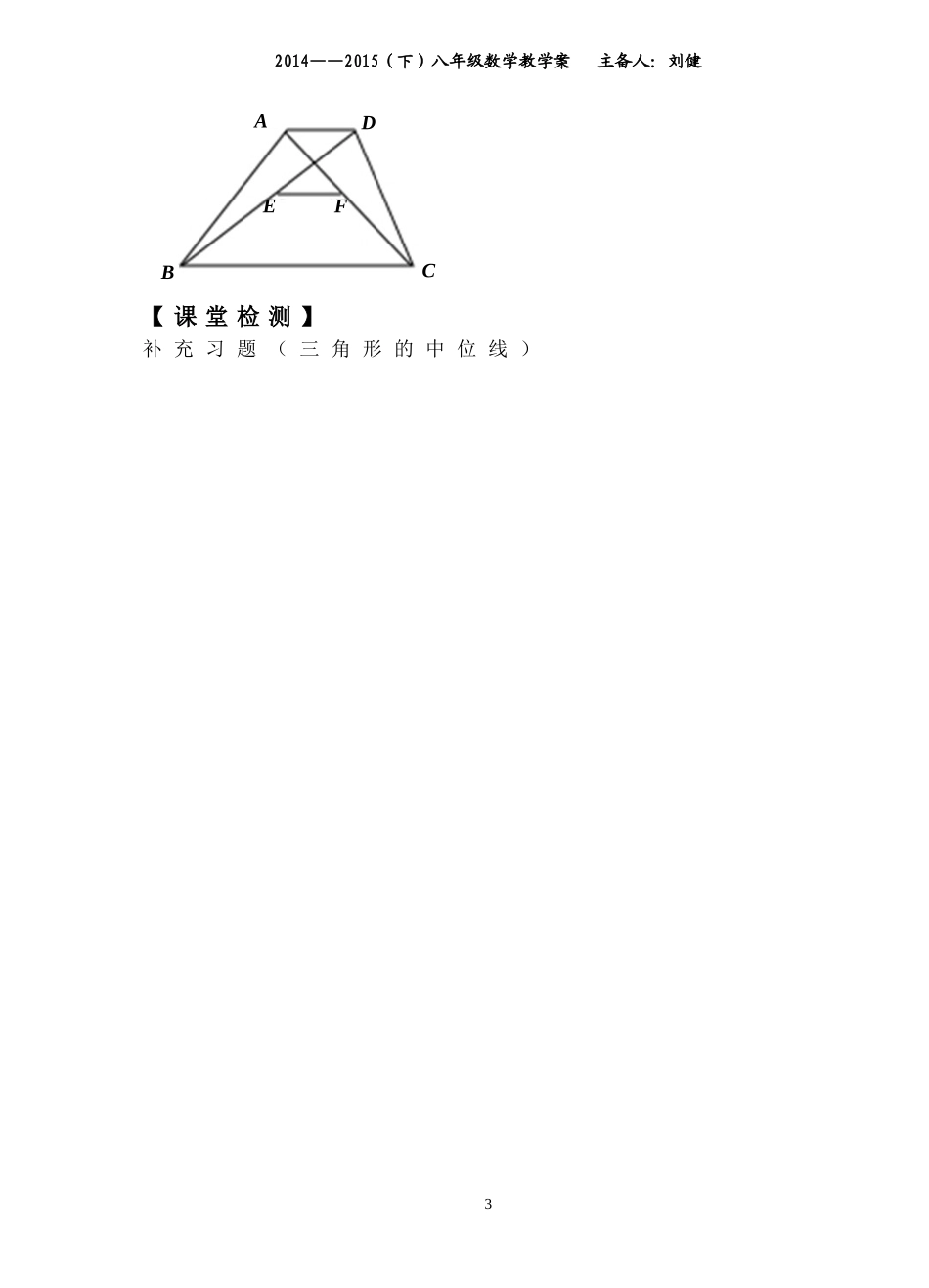
2014——2015(下)八年级数学教学案主备人:刘健9.5三角形的中位线班级姓名【学习目标】1.探索并掌握三角形中位线的概念、性质;2.会利用三角形的中位线的性质解决有关问题;3.经历探索三角形中位线性质的过程,体会转化的思想方法.【学习重点】会利用三角形的中位线的性质解决有关问题.【学习难点】经历探索三角形中位线性质的过程,体会转化的思想方法.【自主预习】1.自学书本P86-87内容.2.如图,A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN=20m,那么A、B两点的距离是m。3.如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,连接EF、EG、FG,那么△EFG是什么三角形?请说明理由.【合作探究】实践探索一操作——观察——探索1.剪一张三角形纸片,记为△ABC;分别取AB、AC的中点D、E,连接DE;沿DE将△ABC剪成两部分,并将△ADE绕点E按顺时针方向旋转180度到△CFE的位置,得四边形BCFD;2.判别四边形BCFD是否是平12014——2015(下)八年级数学教学案主备人:刘健行四边形?并说明理由.3.引入三角形中位线的概念.实践探索二探索三角形中位线的性质.三角形的中位线平行于第三边,并且等于第三边的一半.展示交流一已知:如图,在四边形ABCD中,AB=CD,E、F、G分别是BD、AC、BC的中点.求证:△EFG是等腰三角形.展示交流二已知:在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点.求证:四边形ADEF的周长等于2AB.拓展提高1.已知:如图,梯形ABCD中,AD∥BC,E、F分别是AB、DC的中点.求证:EF∥BC,EF=(BC+AD).用上题的结论完成下题:2.如图,在梯形ABCD中,AD∥BC,E、F分别是对角线BD、AC的中点.若AD=6cm,BC=18cm,求EF的长.ABCDEFGABCDEF22014——2015(下)八年级数学教学案主备人:刘健【课堂检测】补充习题(三角形的中位线)ABCDEF3