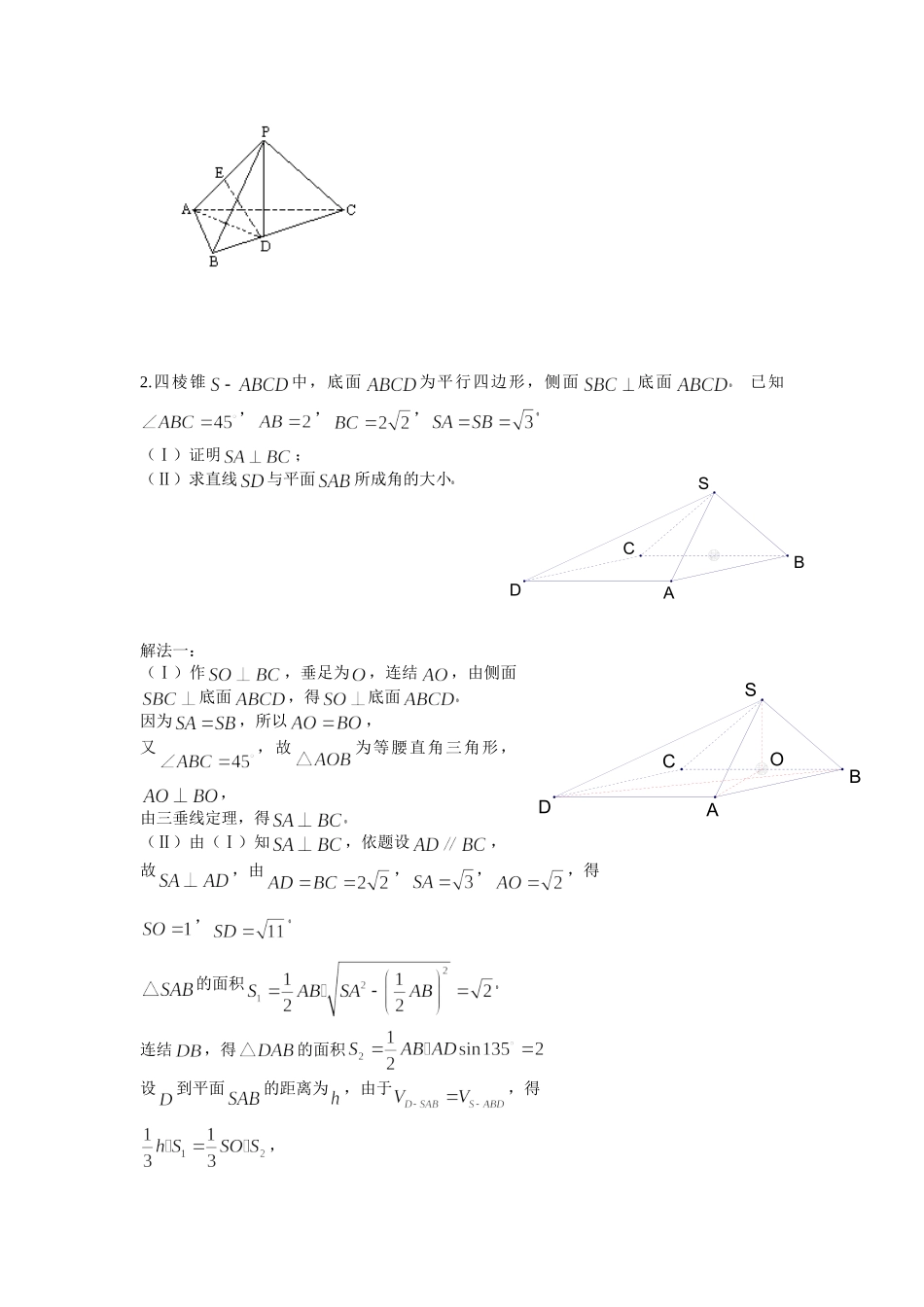
1、如图,三棱锥P—ABC中,已知PA⊥BC,PA=BC=L,PA,BC的公垂线ED=h.证明:连结AD和PD.∵BC⊥PA,BC⊥ED,PA与ED相交,∴BC⊥平面PAD,三棱锥B—PAD体积同理,三棱锥C—PAD的体积∴三棱锥P—ABC体积∵V=V1+V2,若E,D不是分别在线段AP,BC上,结论仍成立.2.四棱锥中,底面为平行四边形,侧面底面·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋已知,,,·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋(Ⅰ)证明;(Ⅱ)求直线与平面所成角的大小·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋解法一:(Ⅰ)作,垂足为,连结,由侧面底面,得底面·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋因为,所以,又,故为等腰直角三角形,,由三垂线定理,得·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋(Ⅱ)由(Ⅰ)知,依题设,故,由,,,得,·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋的面积·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋连结,得的面积设到平面的距离为,由于,得,ABCDOSABCDS解得·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋设与平面所成角为,则·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋所以,直线与平面所成的我为·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋解法二:(Ⅰ)作,垂足为,连结,由侧面底面,得平面·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋因为,所以·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋又,为等腰直角三角形,·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋如图,以为坐标原点,为轴正向,建立直角坐标系,,,,,,,,所以·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋(Ⅱ)取中点,,连结,取中点,连结,·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋,,·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋,,与平面内两条相交直线,垂直·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋所以平面,与的夹角记为,与平面所成的角记为,则与互余·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋,·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋,,所以,直线与平面所成的角为·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋ABCDEGSoxzy3.(1)如图,对于任意给定的四面体,找出依次排列的四个相互平行的,使得且其中每相邻两个平面间的距离都相等;(2)给定依次排列的四个相互平行的平面,其中每相邻两个平面间的距离为,若一个正四面体的四个顶点满足:求该正四面体的体积