内蒙古呼伦贝尔市2012届高三数学总复习《双曲线》课件VIP免费

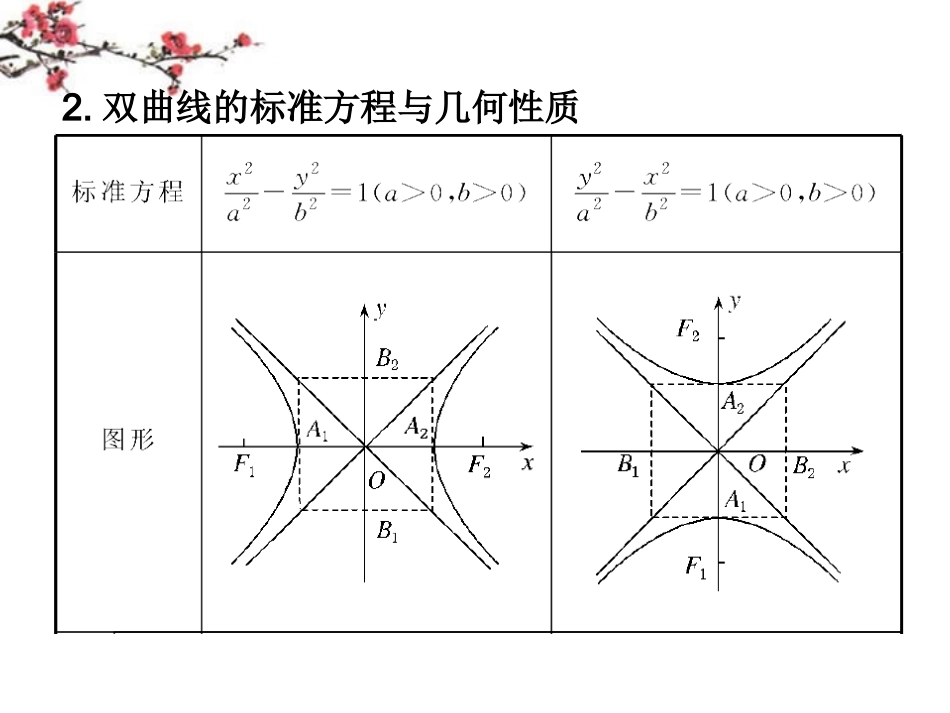
第五十二讲双曲线走进高考第一关考点关回归教材1.双曲线的定义我们把平面内到两定点F1,F2的距离之差的绝对值等于常数(大于零且小于|F1F2|)的点的集合叫做双曲线,定点F1,F2叫做双曲线的焦点,两个焦点之间的距离叫做双曲线的焦距.数学语言:||PF1|-|PF2||=2a(2a<|F1F2|).说明:(1)当2a>|F1F2|时,无轨迹,当2a=|F1F2|时,表示以F1,F2为端点的两条射线(包括端点).2.双曲线的标准方程与几何性质考点训练2222222261.(2009)2xyxyA.1B.12442xyxyC.1D.146410安徽下列曲线中离心率为的是（）答案:B6:Ae3,266Be,B.42解析中中故选22xy2.(2009)1412A.23B.2C.3D.1辽宁双曲线的焦点到渐近线的距离为（）答案:A:y3x,F4,0,43Fd23.A.2解析双曲线的一条渐近线为一个焦点为则焦点到渐近线的距离选222xy3.(2009)1a02,a3a3A.2B.3C.D.12福建若双曲线的离心率为则等于()答案:D22222222222222xy:a1a0,b3,3cab3cab,14,a1.aaa解析解读高考第二关热点关题型一双曲线的几何性质()(,),,,,,_______.2222121221xy120091a0b0abFc0Fc0sinPFFaPsinPFFc例重庆已知双曲线的左、右焦点分别为若双曲线上存在点使则该双曲线的离心率的取值范围是:1e12答案点评:求离心率e的值,要寻找a、b、c之间的等量关系,求e的取值范围,则要寻求a、b、c之间的不等关系,再由不等式求解,在解题过程中要注意数形结合思想.22xy1:e1,e1,2,2mmA.6,0B.0,6C.4,1D.6,1变式设为双曲线的离心率且则实数的取值范围是()答案:A2222222xy:1,2mm0,a2,bm,c2m.2me.e1,2,e1,4.22m14,6m0.2解析为双曲线又故22xy2F1,A1,4,P412,PFPA______.例已知是双曲线的左焦点是双曲线右支上的动点则的最小值为答案:92111112211min:a4,2a4.F.PF|PF|2a,PF|PF|4.PFPA|PFPA|4,PAF|PFPA|,(|PFPA|)4145,PFPA549.解析根据双曲线方程知设为右焦点再由双曲线定义知的最小值化为求的最小值显然当是线段与双曲线右支交点时取得最小值最小值为点评:要灵活运用双曲线的定义,将双曲线上的点到两焦点的距离相互转化,从而解决问题.221222121222222x2:F,F1a0,b0ab,M,FMFN,|FNNF|abA.bB.aC.cD.ay变式已知分别为双曲线的左、右焦点为双曲线上除顶点外的任意一点且的内切圆交实轴于点则的值为()答案:A解析:由已知得|MF1|-|MF2|=±2a,作图,易知|F1N|-|NF2|=±2a,又|F1N|+|NF2|=2c,|F∴1N|=c+a或c-a,|NF2|=c-a或c+a.因此|F1N|5|NF2|=(c+a)(c-a)=c2-a2=b2.题型二双曲线的标准方程例3已知过点P(0,-2)的双曲线C的一个焦点与抛物线x2=-16y的焦点相同,则双曲线C的标准方程是()22222222xyyxA.1B.1124412xyyxC.1D.1204420答案:B22222:0,4,y,c4,P0,2,yxa2,bca12,1.412解析由抛物线方程得其焦点坐标为据此可得双曲线焦点在轴上且又双曲线过点故因此故双曲线方程为点评:根据条件求双曲线方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选取方程的形式,当焦点不能定位时,则应分两种情况讨论.变式3:如图,已知双曲线以长方形ABCD的顶点A、B为左、右焦点,且过C、D两点,若AB=4,BC=3,则此双曲线的标准方程为________.22y:x13答案:,,,,.22c22aDBDA532ya1b3x13解析由题意知故标准方程为例4已知A(1,0),B(-2,0),动点M满足∠MBA=2MAB(MAB≠0).∠∠求动点M的轨迹E的方程.点评:求点的轨迹方程,常用的方法是直接法,即根据动点运动的条件得到几何量的等量关系,但一定要注意变量的取值范围.变式4:已知两个定圆O1和O2,它们的半径分别是1和2,且|O1O2|=4.动圆M与圆O1内切,又与圆O2外切,建立适当的坐标系,求动圆圆心M的轨迹方程,并说明轨迹是何种曲线.1212121211221122222:,OOO,OOx.|OO|4,O2,0,O2,0.Mr,MO,|MO|r1;MO2,|MO|r2.|MOMO|3.MO,O,3.37a,c2,bca.244xM9解如图所示以的中点为...