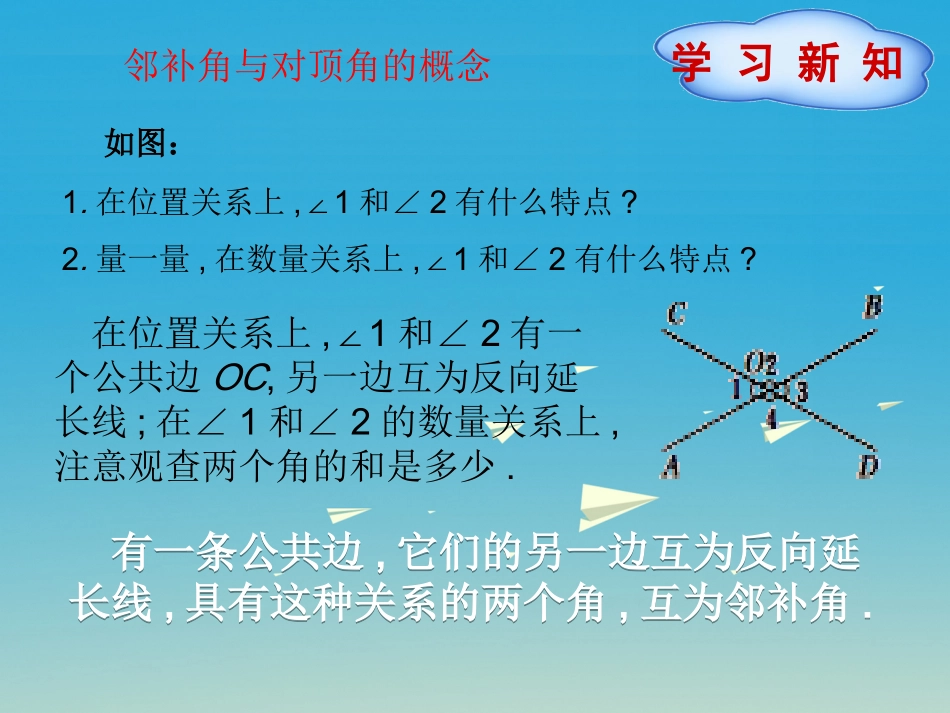
七年级数学·下新课标[人]第五章相交线与平行线学习新知检测反馈5.1.1相交线如图所示,要想测量两堵围墙所形成的∠AOB的度数(人不能进入围墙内,又不能站在围墙上),甲、乙两人各有如下的测量方法:甲:延长AO至C,测得∠BOC的度数,可知∠AOB的度数.乙:延长AO至C,延长BO至D,测得∠COD的度数,可知∠AOB的度数.你知道他们这样测量的道理吗?观察思考观察思考如图:1.在位置关系上,1∠和∠2有什么特点?2.量一量,在数量关系上,1∠和∠2有什么特点?学习新知在位置关系上,1∠和∠2有一个公共边OC,另一边互为反向延长线;在∠1和∠2的数量关系上,注意观查两个角的和是多少.有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.邻补角与对顶角的概念有四组邻补角,分别是∠1和∠2,2∠和∠3,∠3和∠4,1∠和∠4想一想(1)如图:图中有几组邻补角?(2)在图中,剪刀把手之间角度变化的过程中,这种关系还存在吗?这种关系依旧存在.在位置关系上,1∠和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线;(2)通过测量和观察,学生可以发现∠1和∠3是相等的.(1)看一看在位置上,1∠和∠3有什么特点?(2)量一量,在数量关系上,1∠和∠3有什么特点?有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.(1)在图中有哪些角是对顶角?(2)观察、测量每组对顶角,它们之间有什么数量关系?(3)根据观察和测量,你的结论是什么?怎样去证明你的结论?〔解析〕如图所示,∠AOC和∠AOD互补,∠AOC和∠BOC互补,由“同角的补角相等”,可以得出∠AOD=∠BOC,类似地,∠AOC=∠BOD.这样,我们就得到了对顶角的性质:对顶角相等.证明:因为∠AOC和∠AOD互补,∠AOC和∠BOC互补(邻补角的定义),所以∠AOD=∠BOC(同角的补角相等).例:如图所示,直线a,b相交,1=40°,∠求∠2,3,4∠∠的度数.解:由邻补角的定义,得:∠2=180°-1=180°-40°=140°∠由对顶角相等,得:∠3=1=40°,4=2=140°∠∠∠.解析:计算角的度数,首先要考虑给定的角与所要求的角的位置关系和数量关系.从位置关系看,在要求的三个角中,∠3和∠1存在着对顶角的关系,∠2,∠4和∠1存在着邻补角的关系.解析:计算角的度数,首先要考虑给定的角与所要求的角的位置关系和数量关系.从位置关系看,在要求的三个角中,∠3和∠1存在着对顶角的关系,∠2,∠4和∠1存在着邻补角的关系.例:(补充)如图所示,已知直线AB与CD相交于点O,OE是∠BOD的平分线,∠EOF=90°,若∠BOD=58°,求∠COF的度数.解:因为OE是∠BOD的平分线,∠BOD=58°,所以2∠DOE=∠BOD=58°所以∠DOE=29°,因为∠EOF=90°,所以∠DOF=∠EOF-∠DOE=90°-29°=61°所以∠COF=180°-∠DOF=180°-61°=119°.解析:根据角平分线的定义求出∠DOE,再求出∠DOF,然后根据邻补角的定义列式计算即可得解.解析:根据角平分线的定义求出∠DOE,再求出∠DOF,然后根据邻补角的定义列式计算即可得解.[解题策略]本题考查了角平分线的定义,互为邻补角的两个角的和等于180°,熟记概念并准确识图,理清图中各角度之间的关系是解题的关键.[解题策略]本题考查了角平分线的定义,互为邻补角的两个角的和等于180°,熟记概念并准确识图,理清图中各角度之间的关系是解题的关键.1.邻补角、对顶角的概念:(1)有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.(2)有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.(3)邻补角、对顶角是成对出现的,在相交直线中,一个角的邻补角有两个.课堂小结课堂小结2.邻补角、对顶角的性质:(1)邻补角互补.但两个角的和等于180°,这两个角不一定是邻补角.(2)对顶角相等.但反过来,相等的两个角不一定是对顶角.检测反馈1.如图所示,下列判断正确的是()A.图(1)中∠1和∠2是一组对顶角B.图(2)中∠1和∠2是一组对顶角C.图(3)中∠1和∠2是一组邻补角D.图(4)中∠1和∠2是一组邻补角解析:对顶角的定义:...