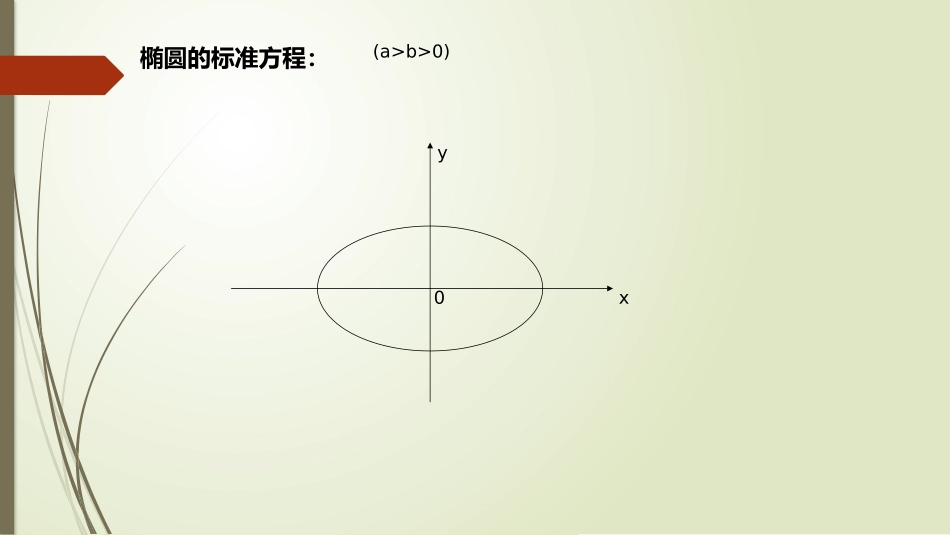
椭圆的几何性质金坛一中景庆教学目标:1、通过对椭圆的标准方程和图像的分析,理解并掌握椭圆的范围、对称性、顶点、离心率。2、会根据所给椭圆的方程,写出其范围、对称性、顶点、离心率。、3、理解椭圆离心率是用来刻画椭圆的“圆扁”程度,会根据所给条件找出a,b,c的关系,并求出离心率。4、掌握利用代数式研究圆锥曲线几何性质的方法。椭圆的标准方程:(a>b>0)yx01、范围:由椭圆方程(a>b>0)可知:椭圆上任意一点的坐标(x,y)都满足即,所以-a,同理可得-b,问题1:这一性质在图像上有何特征?yx0说明椭圆位于直线x=所围成的矩形内2、对称性:问题2:在椭圆的标准方程中,把x换成-x方程并不变,这说明什么?yx0P(x,y)P1(-x,y)yx0P(x,y)P1(-x,y)P2(x,-y)P3(-x,-y)总结:椭圆是轴对称图形,对称轴为坐标轴;椭圆也是中心对称图形,对称中心为原点,也称为椭圆的中心。3、顶点:椭圆与坐标轴的四个交点:A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)称为椭圆的顶点。其中线段A1A2,B1B2分别叫做椭圆的长轴和短轴,它们的长分别为2a和2b,a和b分别叫做椭圆的长半轴长和短半轴长。,4、离心率:问题、椭圆有的比较“扁”,有的比较“圆”,怎样来刻画椭圆的“扁”的程度呢?探究:(同学操作,交流讨论)1、将细绳的两端点固定在焦点处,改变绳长,观察椭圆的“扁”的程度?2、细绳的长度不变,将焦距增大或缩小,观察椭圆的“扁”的程度?总结:叫做椭圆的离心率,记为e。(1)因为0