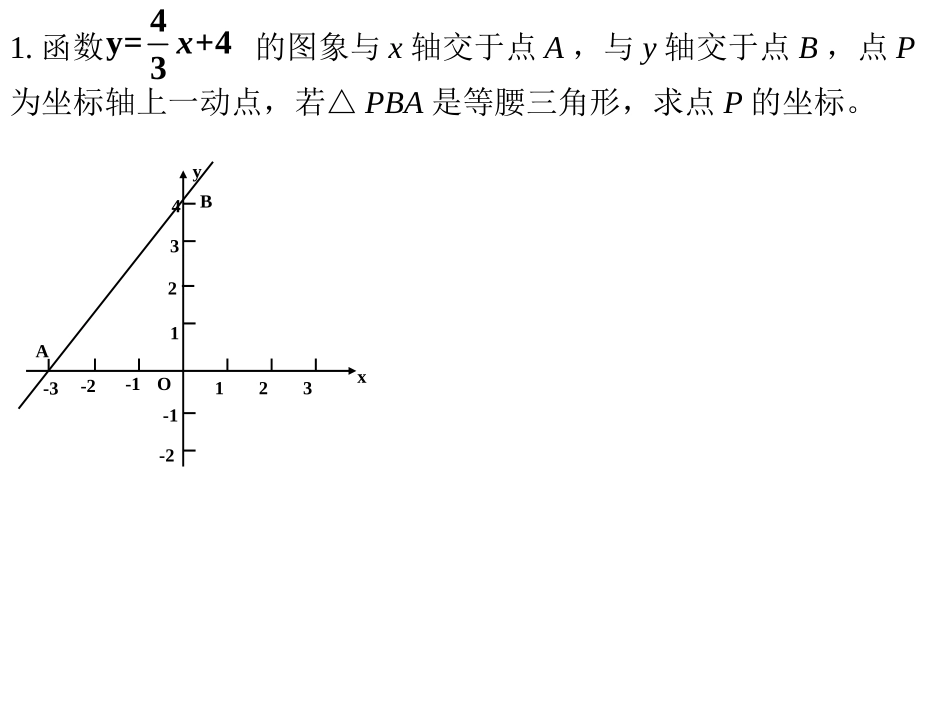
天下无难事,有志者成之天下无易事,有恒者得之等腰三角形分类讨论一.当腰长和底边长不能确定时,必须进行分类讨论3.等腰三角形一腰上的高与另一边的夹角为25°,求这个三角形的各个内角的度数。三.当高的位置关系不确定时,必须进行分类讨论2.已知等腰三角形的一个内角为80°,则另两个角的度数是.二.当顶角和底角不能确定时,必须进行分类讨论1.等腰三角形的两边长是3和5,它的周长是.11或1350°,50°或80°,20°65°,67.5°,67.5°或115°,32.5°,32.5°OA123-324-1-2xyB13-2-11.函数的图象与x轴交于点A,与y轴交于点B,点P为坐标轴上一动点,若△PBA是等腰三角形,求点P的坐标。4y=+43xOA123-324-1-2xyB13-2-1变式1:函数的图象与x轴交于点A,与y轴交于点B,点P为直线AB上一动点,若△POA是等腰三角形,求点P的坐标。4y=+43x2.如图,已知直线l1的解析式为y=3x+6,直线l1与x轴、y轴分别相交于A、B两点,直线l2经过B、C两点,点C的坐标为(8,0)又已知点P在x轴上从点A向点C移动,点Q在直线l2从点C向点B移动。点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(0