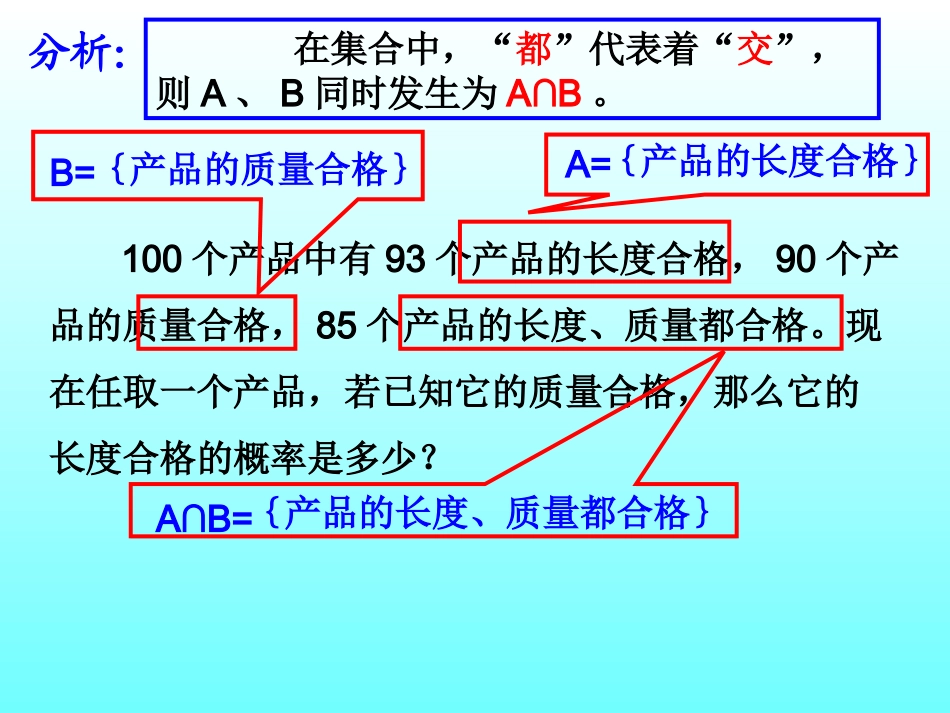
100个产品中有93个产品的长度合格,90个产品的质量合格,85个产品的长度、质量都合格。现在任取一个产品,若已知它的质量合格,那么它的长度合格的概率是多少?实例探究问题一:100个产品中有93个产品的长度合格,90个产品的质量合格,85个产品的长度、质量都合格。现在任取一个产品,若已知它的质量合格,那么它的长度合格的概率是多少?A={产品的长度合格}B={产品的质量合格}A∩B={产品的长度、质量都合格}在集合中,“都”代表着“交”,则A、B同时发生为A∩B。分析:任取一个产品,已知它的质量合格(即B发生),则它的长度合格(即A发生)的概率是。9085思考:由已知可得:容易发现:这个概率与事件A、B的概率有什么关系么?10085)(,10090)(,10093)(BAPBPAP)()(10090100859085BPBAP概括求B发生的条件下,A发生的概率,称为B发生时A发生的条件概率,记为。)(BAP当时,,其中,0)(BP)()()(BPBAPBAPBA可记为。AB类似地时,。0)(AP)()()(ABPABPAPA发生时B发生的概率1.某种动物出生之后活到20岁的概率为0.7,活到25岁的概率为0.56,求现年为20岁的这种动物活到25岁的概率。解:设A表示“活到20岁”(即≥20),B表示“活到25岁”(即≥25)则()0.7,()0.56PAPB所求概率为()()()0.8()()PABPBPBAPAPAAB0.560.7问题二:从一副扑克牌(去掉大小王)中随机抽取1张,用A表示“取出牌“Q””,用B表示“取出的是红桃”,是否可以利用来计算?)(),(ABPBP)(BAP分析:剩余的52张牌中,有13张红桃,则415213)(BP52张牌中红桃Q只有1张,则521)(ABP由条件概率公式知,当取出牌是红桃时为Q的概率为:131)()()(BPABPBAP我们知道52张牌中有4个Q,所以:131524)(AP易看出此时:)()(APBAP而此时有:)()()(BPAPABP说明事件B的发生不影响A的发生你能举出生活中的一些独立生活的例子么??概括总结一般地,两个事件、,若有,则称、相互独立。AABB)()()(BPAPABP或者说A的发生与B的发生互不影响。判断:下列哪些事件相互独立。①篮球比赛的“罚球两次”中,事件A:第一次罚球,球进了;事件B:第二次罚球,球进了。②在三月份的月考较量中,事件A:同学甲获得第一名;事件B:同学乙获得第一名。③袋中有三个红球,两个白球,采取不放回的取球,事件A:第一次从中任取一个球是白球;事件B:第二次从中任取一个球是白球。④甲坛子里有3个红球,2个黄球,乙坛子里也有3个红球,2个黄球,从这两个坛子里分别摸出1个球事件A:从甲坛子里摸出1个球,得到黄球;事件B:从乙坛子里摸出1个球,得到黄球。例1调查发现,某班学生患近视的概率为0.4,现随机抽取该班级的2名同学进行体检,求他们都近视的概率。例题分析解:记A为甲同学近视,B为乙同学近视,则A、B相互独立,且,则4.0)()(BPAP)()()(BPAPABP16.04.04.0推广:对于n个相互独立的事件,则有nAAA,,,21)()()()(2121nnAPAPAPAAAP前面讨论了两个相互独立事件的概率公式,若、相互独立,则有AB)()()(BPAPABP事实上,对于多个独立事件,公式也是成立的。将一枚均匀硬币掷4次,有人认为:“第一次出现正面,第二次出现反面,第三次出现正面,第四次出现反面”发生的概率比“四次都出现正面”的概率大,你认为这种说法正确么?思考讨论:小结当时,。0)(BP)()()(BPBAPBAP*条件概率:当事件B发生时,事件A发生的概率:*独立事件的概率:若A的发生与B的发生互不影响,称A、B相互独立。A、B同时发生的概率:)()()(BPAPABP对于n个相互独立的事件,则有nAAA,,,21)()()()(2121nnAPAPAPAAAP作业:甲、乙二人各进行1次射击比赛,如果2人击中目标的概率都是0.6,计算:(1)2人都击中目标的概率;(2)其中恰有1人击中目标的概率;(3)至少有一人击中目标的概率。谢谢!