4解直角三角形VIP免费

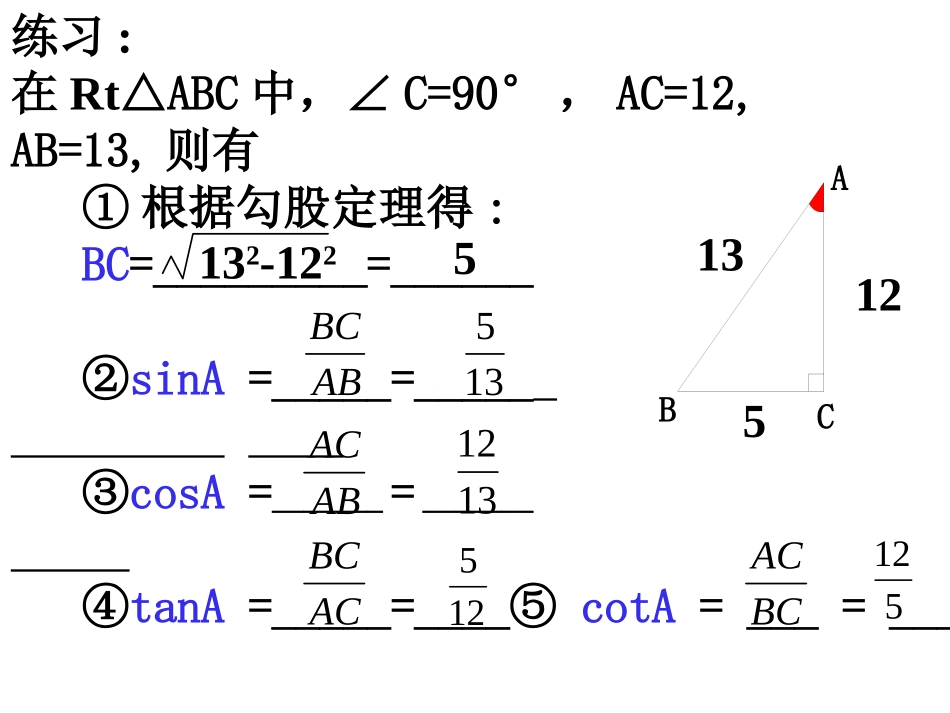
直角三角形三边之间关系锐角之间关系边角之间关系(以锐角A为例)图19.3.1a2+b2=c2（勾股定理）∠A+B=90º∠ABBCAA斜边的对边sinABACAA斜边的邻边cosACBCAAA的邻边的对边tanBCACAAA的对边的邻边cot练习:在Rt△ABC中，∠C=90°，AC=12,AB=13,则有①根据勾股定理得:BC=_________=______②sinA=_____=_____③cosA=_______=_______④tanA=_____=____⑤cotA=___=___51351312125512132-122ABC12135ABBCABACACBCBCAC例1.如图所示，一棵大树在一次强烈的地震中于离地面10米处折断倒下，树顶落在离树根24米处.大树在折断之前高多少？解利用勾股定理可以求出折断倒下部分的长度为:26＋10＝36（米）.答:大树在折断之前高为36米.22102426+=例2如图，在Rt△ABC中，∠C＝90°，解这个直角三角形6,2BCAC解：326tanACBCA60A30609090AB222ACABABC261.在Rt△ABC中，∠C＝90°，根据下列条件解直角三角形；（1）a=30,b=20;解：根据勾股定理222230201013Cab303tan1.5202aAb56.3A909056.333.7BAABCb=20a=30c随堂练习2.在电线杆离地面8米高的地方向地面拉一条长10米的缆绳，问这条缆绳应固定在距离电线杆底部多远的地方？8米10米?BCA1.在直角三角形中，由已知元素求出未知元素的过程，叫做解直角三形；3.在直角三角形中，如果已知两条边的长度，那么就可利用勾股定理求出另外的一条边.2.在解决实际问题时,应“先画图,再求解”；概括4.在直角三角形中，如果已知两条边的长度，能否求出另外两个锐角？解直角三角形，只有下面两种情况：（1）已知两条边；（2）已知一条边和一个锐角．（2）两锐角之间的关系∠A＋∠B＝90°（3）边角之间的关系caAA斜边的对边sincbBB斜边的对边sincbAA斜边的邻边coscaBB斜边的邻边cosbaAAA的邻边的对边tanabBBB的邻边的对边tan（1）三边之间的关系222cbaABabcC在解直角三角形的过程中，一般要用到的一些关系：例3如图，在Rt△ABC中，∠B＝35°，b=20，解这个直角三角形（精确到0.1）解：∠A＝90°－∠B＝90°－35°＝55°abBtan6.2870.02035tan20tanBbacbBsin1.3557.02035sin20sinBbcABCabc2035°你还有其他方法求出c吗？例4如图，在Rt△ABC中，∠C＝90°，AC=6，∠BAC的平分线，解这个直角三角形.43ADDABC643解：63cos243ACCADAD30CAD因为AD平分∠BAC60,30CABB12,63ABBC1.在Rt△ABC中，∠C＝90°，根据下列条件解直角三角形；∠B＝72°，c=14.ABCbac=14解：sinbBcsin14sin7213.3bcB907218AcosaBccos14cos724.34acB随堂练习课堂小结1.定义：在直角三角形中，由已知元素求出未知元素的过程，叫做解直角三角形;2.在解决实际问题时,应“先画图,再求解”;