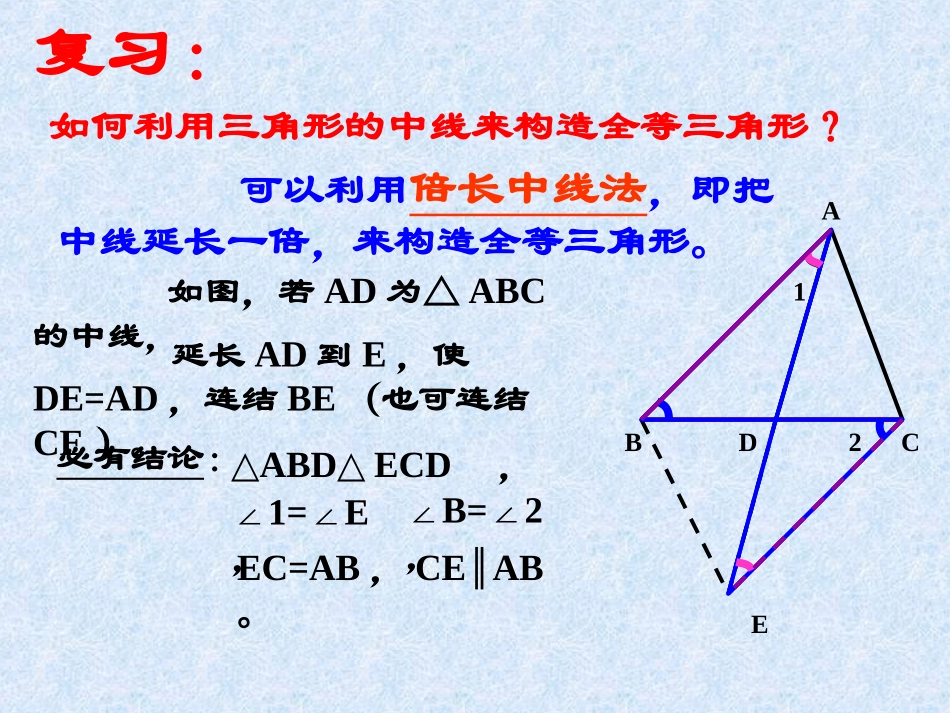
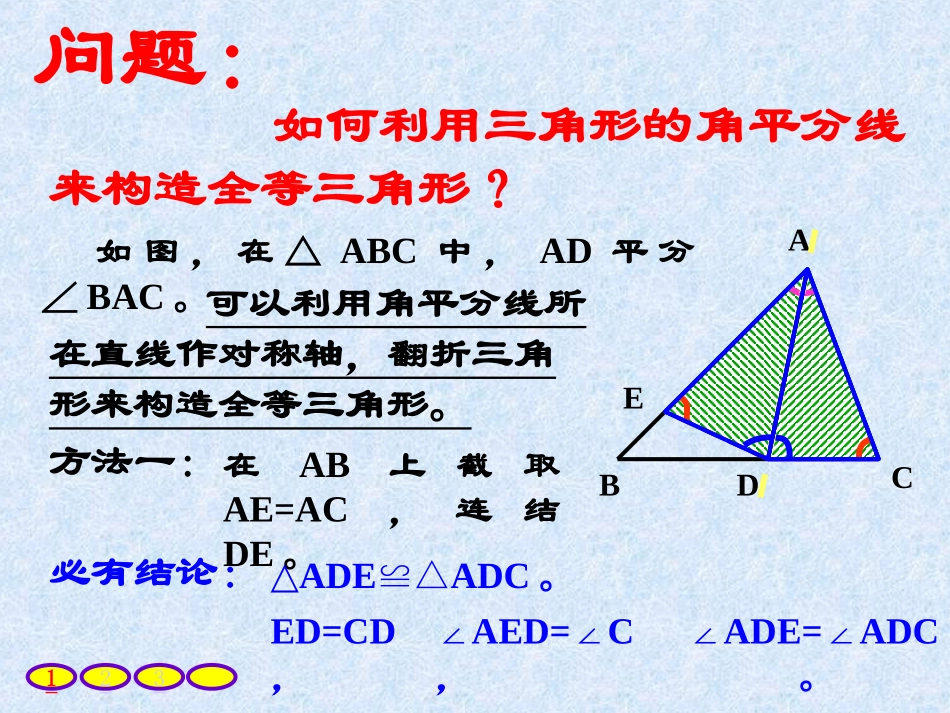
如何利用三角形的中线来构造全等三角形?复习:可以利用倍长中线法,即把中线延长一倍,来构造全等三角形。如图,若AD为△ABC的中线,必有结论:ABCDE12延长AD到E,使DE=AD,连结BE(也可连结CE)。△ABDECD△,∠1=E∠,∠B=2∠,EC=AB,CEAB∥。可以利用角平分线所在直线作对称轴,翻折三角形来构造全等三角形。如何利用三角形的角平分线来构造全等三角形?问题:如图,在△ABC中,AD平分∠BAC。方法一:ABCDE必有结论:在AB上截取AE=AC,连结DE。△ADEADC≌△。ED=CD,321∠AED=C∠,∠ADE=ADC∠。方法二:ABCDF延长AC到F,使AF=AB,连结DF。必有结论:△ABDAFD≌△。BD=FD,如何利用三角形的角平分线来构造全等三角形?问题:321如图,在△ABC中,AD平分∠BAC。可以利用角平分线所在直线作对称轴,翻折三角形来构造全等三角形。∠B=F∠,∠ADB=ADF∠。如何利用三角形的角平分线来构造全等三角形?问题:ABCDMN方法三:过点D作DMAB⊥于M,DNAC⊥于N。必有结论:△AMDAND≌△。DM=DN,321如图,在△ABC中,AD平分∠BAC。可以利用角平分线所在直线作对称轴,翻折三角形来构造全等三角形。AM=AN,∠ADM=AND∠。(还可以用“角平分线上的点到角的两边距离相等”来证DM=DN)证明:例1已知:如图,在四边形ABCD中,BD是∠ABC的角平分线,AD=CD,求证:∠A+∠C=180°DABCE(方法一)在BC上截取BE,使BE=AB,连结DE。 BD是∠ABC的角平分线,∴∠1=2.∠在△ABD和△EBD中AB=EB, ∠1=2,∠BD=BD,∴△ABDEBD≌△(SAS)1243 ∠3+4∠=180°,∴∠A+C∠=180°321∴∠A=∠3,AD=DE AD=CDDE=DC∴∴∠4=C∠(等边对等角)证明:例1已知:如图,在四边形ABCD中,BD是∠ABC的角平分线,AD=CD,求证:∠A+∠C=180°DABCF(方法二)延长BA到F,使BF=BC,连结DF。 BD是∠ABC的角平分线∴∠1=2∠在△BFD和△BCD中BF=BC ∠1=2∠BD=BD∴△BFDBCD≌△(S.A.S)1243 ∠F=∠C,∴∠4=C∠。321∴∠F=∠C,DF=DC AD=CD,∴DF=AD∴∠4=F∠(等边对等角) ∠DAB+4∠=180°,∴∠DAB+C∠=180°。证明:例1已知:如图,在四边形ABCD中,BD是∠ABC的角平分线,AD=CD,求证:∠A+∠C=180°DABCM(方法三)过点D作DMBC⊥于M,DNBA⊥交BA的延长线于N。 BD是∠ABC的角平分线,∴∠1=2∠。 DNBA⊥,DMBC⊥,∴∠N=DMB=90°∠。在△NBD和△MBD中 ∠N=DMB,∠∠1=2,∠BD=BD,12N43321△NBDMBD≌△(AAS)∴ND=MD例1已知:如图,在四边形ABCD中,BD是∠ABC的角平分线,AD=CD,求证:∠A+∠C=180°DABCM12N43321 DNBA⊥,DMBC⊥,∴∠N=DMC=90°∠。在RtNAD△和RtMCD△中 ND=MD,AD=CD,∴RtNADRtMCD△≌△(HL)∴∠4=C∠, ∠DAB+4∠=180°,∴∠DAB+C∠=180°。证明:例1已知:如图,在四边形ABCD中,BD是∠ABC的角平分线,AD=CD,求证:∠A+∠C=180°DABCM(方法四)过点D作DMBC⊥于M,DNBA⊥交BA的延长线于N。12N43321 BD是∠ABC的角平分线,DNBA⊥,DMBC⊥,∴ND=MD。∴∠4=C∠ DNBA⊥,DMBC⊥,∴∠AND和∠CMD=90°在RtNAD△和RtMCD△中 ND=MD,AD=CD,∴RtNADRt△≌MCD△(HL) ∠DAB+4∠=180°,∴∠DAB+C∠=180°.练习1如图,已知△ABC中,AD是∠BAC的角平分线,AB=AC+CD,求证:∠C=2∠BABCDE1221证明:在AB上截取AE,使AE=AC,连结DE。 AD是∠BAC的角平分线,∴∠1=2∠。在△AED和△ACD中 AE=AC,∠1=2∠,AD=AD,∴△AEDACD≌△(S.A.S)3∴∠B=4∠(等边对等角)4∴∠C=∠3,ED=CD AB=AC+CD=AE+EB,∴EB=DC=ED。 ∠3=B+4=2B∠∠∠,∴∠C=2B∠。练习1如图,已知△ABC中,AD是∠BAC的角平分线,AB=AC+CD,求证:∠C=2∠BABCDF12证明:延长AC到F,使CF=CD,连结DF。 AD是∠BAC的角平分线,∴∠1=2∠。 AB=AC+CD,CF=CD,∴AB=AC+CF=AF。 ∠ACB=F+3=2F∠∠∠,∴∠ACB=2B∠。321在△ABD和△AFD中 AB=AF,∠1=2∠,AD=AD,∴△ABDAFD≌△(SAS)。∴∠F=∠B, CF=CD,∴∠B=3∠(等边对等角)练习2如图,已知直线MN∥PQ,且AE平分∠BAN、BE平分∠QBA,DC是过E的任意线段,交MN于点D,交PQ于点C。求证:AD+AB=BC。证明:延长AE,交直线PQ于点F。30*21ABCDEMNPQ1234F5练习2如图,已知直线...