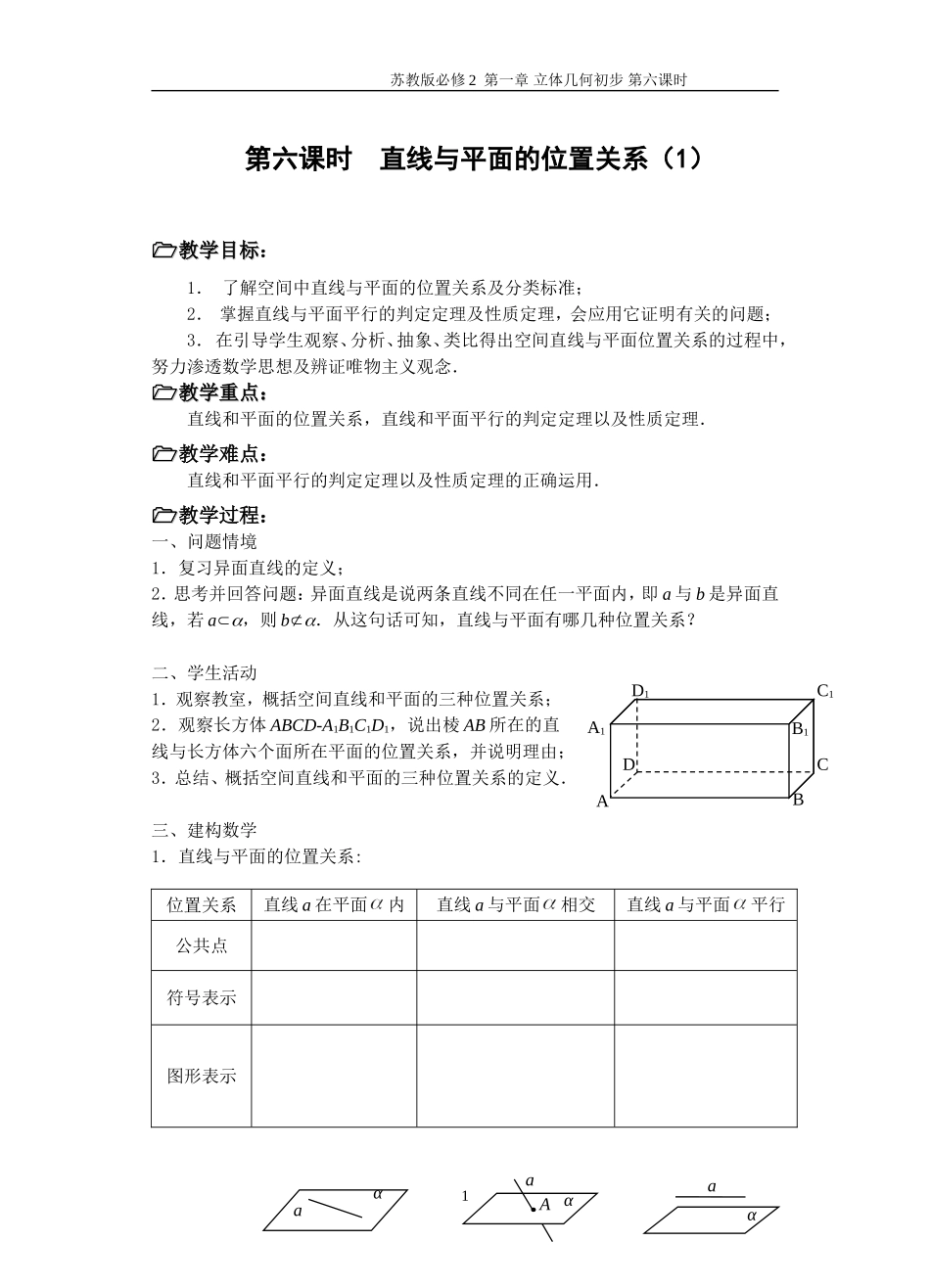
苏教版必修2第一章立体几何初步第六课时第六课时直线与平面的位置关系(1)教学目标教学目标:1.了解空间中直线与平面的位置关系及分类标准;2.掌握直线与平面平行的判定定理及性质定理,会应用它证明有关的问题;3.在引导学生观察、分析、抽象、类比得出空间直线与平面位置关系的过程中,努力渗透数学思想及辨证唯物主义观念.教学重点:教学重点:直线和平面的位置关系,直线和平面平行的判定定理以及性质定理.教学难点:直线和平面平行的判定定理以及性质定理的正确运用.教学过程:一、问题情境1.复习异面直线的定义;2.思考并回答问题:异面直线是说两条直线不同在任一平面内,即a与b是异面直线,若aÌa,则bËa.从这句话可知,直线与平面有哪几种位置关系?二、学生活动1.观察教室,概括空间直线和平面的三种位置关系;2.观察长方体ABCD-A1B1C1D1,说出棱AB所在的直线与长方体六个面所在平面的位置关系,并说明理由;3.总结、概括空间直线和平面的三种位置关系的定义.三、建构数学1.直线与平面的位置关系:位置关系直线a在平面内直线a与平面相交直线a与平面平行公共点符号表示图形表示1BB1ADCD1C1A1αaαaAaαHGFEBADCα苏教版必修2第一章立体几何初步第六课时注:直线a与平面α相交和平行的情况统称为直线在平面外,记作:2.直线与平面平行的判定定理:符号语言:图形语言:简记为:注:要证明线面平行关键在于在平面内找到一条线与已知直线平行;3.直线和平面平行的性质定理:符号语言:图形语言:简记为:注:线面平行性质定理的运用关键在于过平面外的直线构造辅助平面与已知平面相交,则有已知直线与交线平行;四、数学运用例1如图,已知E、F分别是三棱锥A-BCD的侧棱AB、AD的中点,求证:EF∥平面BCD.例2如图,已知异面直线AB,CD都与平面平行,CA,CB,DB,DA分别交于点E,F,G,H.[求证:四边形EFGH是平行四边形.2ADBCEFDEMABCNP苏教版必修2第一章立体几何初步第六课时例3M,N,P分别为空间四边形ABCD的边AB,BC,CD上的点,且AM:MB=CN:NB=CP:PD.求证:⑴AC∥平面MNP,BD∥平面MNP;⑵平面MNP与平面ACD的交线∥AC.巩固练习:1.如果两直线a∥b,且a∥平面α,则b与α的位置关系是.2.过平面外一点,与这个平面平行的直线有条.3.P是两条异面直线a、b外一点,过点P可作个平面与a、b都平行.4.如图所示,P是平行四边形ABCD所在平面外一点,E,F分别在PA,BD上,且PE∶EA=BF∶FD.求证:EF∥平面PBC.课堂小结:本节课学习了以下内容:1.线面平行的判定定理:线线平行线面平行;2.线面平行的性质定理:线面平行线线平行;3.线面平行判定定理在使用时通常要在平面内找到一条线与已知直线平行;而线面平行的性质定理在使用时则需要构造辅助面找到交线,从而得到线线平行.3PFEDCBA