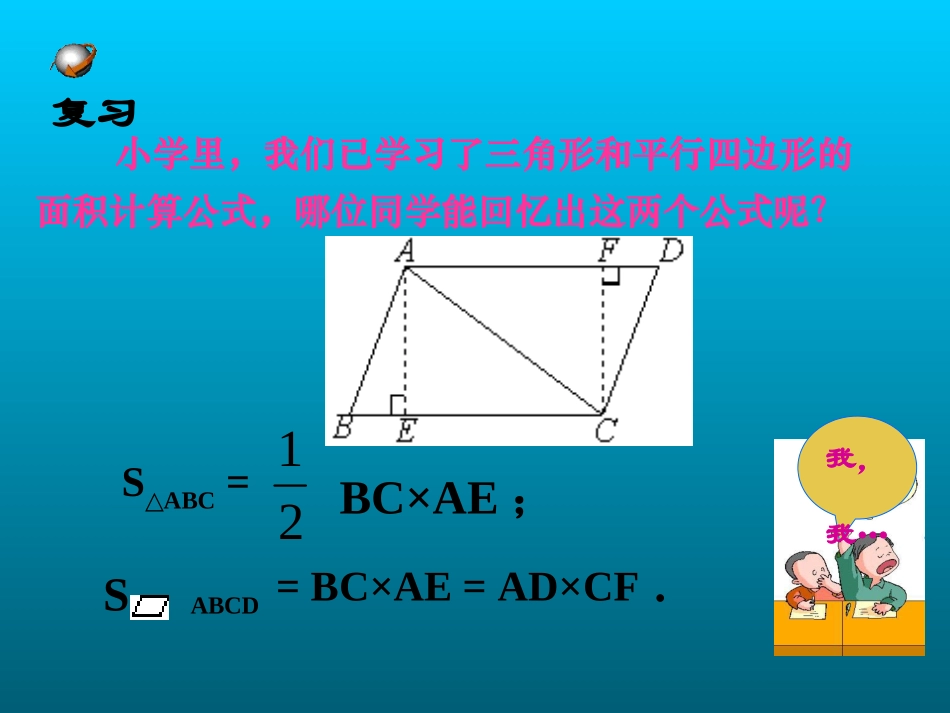
18.1.3平行四边形的性质(三)引言数学中的一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏的极深.——高斯小学里,我们已学习了三角形和平行四边形的面积计算公式,哪位同学能回忆出这两个公式呢?我,我…21SABC△=BC×AE;ABCD=BC×AE=AD×CF.S复习如图,已知直线mn∥,A、B为直线n上两点,C、P为直线m上两点.(1)请写出图中面积相等的三角形.(2)如果A、B、C为三个定点,点P在m上移动,那么,无论P点移动到任何位置,总有与△ABC的面积相等.理由是.创设意境,探究归纳结论:感悟与收获(1)“同底(或等底)等高的三角形面积相等”.(2)“三角形的面积等于与它同底等高平行四边形面积的一半”.创设意境,探究归纳设平行四边形的面积为S.如图(1)AC为ABCD的对角线,试用S来表示△ABC和△CDA的面积.如图(2)E为BC上任一点,试用S来表示△AED的面积.如图(3)E为BC的中点,F为AB的中点,试用S表示△DEF的面积.例1实践应用,典型例题例2已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高为h.“若点P在一边BC上,如图(1),此时,h3=0,可得出结论h1+h2+h3=h.”请直接应用上述信息解决下列问题:当点P在△ABC内(如图(2))、点P在△ABC外(如图(3))这两种情况时,上述结论是否仍成立?若成立,请给予说明;若不成立,h1、h2、h3与h之间又有怎样的关系,请写出你的猜想,不需说明.实践应用,典型例题例3如图,田村有一口呈四边形的池塘,在它的四个角A、B、C、D处均种有一棵梨树,田村准备开始挖池塘建养鱼池,想使建后的鱼池面积为原来池塘面积的两倍,又想保持梨树不动,并要求建后的池塘成为平行四边形形状.请问田村能否实现这一设想?若能,请你设计并画出图形,若不能,请说明理由(画图保留痕迹,不写画法).实践应用,典型例题在研究同底等高的平行四边形和在研究同底等高的平行四边形和三角形的面积的联系问题中,应寻找三角形的面积的联系问题中,应寻找平行四边形和三角形的底、平平行四边形和三角形的底、平行四边形和三角形的高之间的关系,行四边形和三角形的高之间的关系,再利用面积公式进行有关的计算.再利用面积公式进行有关的计算.小结1.如图,点P为四边形的边CD上一个动点,当四边形ABCD满足什么条件时,△PAB的面积始终保持不变(只需补充你认为正确的一种条件即可,不必考虑所有可能的条件)?演练2.如图,ABCD的对角线AC、BD交于点O,试说明AC、BD把平行四边形分成的四个三角形面积相等.若点E是AC上任意一点,可进一步得出哪些三角形的面积相等?演练3.等腰△ABC中,D是BC上任一点,过点D作DEAB⊥于E、过点D作DFAC⊥于F、过点B作BGAC⊥于G,试说明BG=DF+DE.演练选用课时作业设计.作业结束寄语