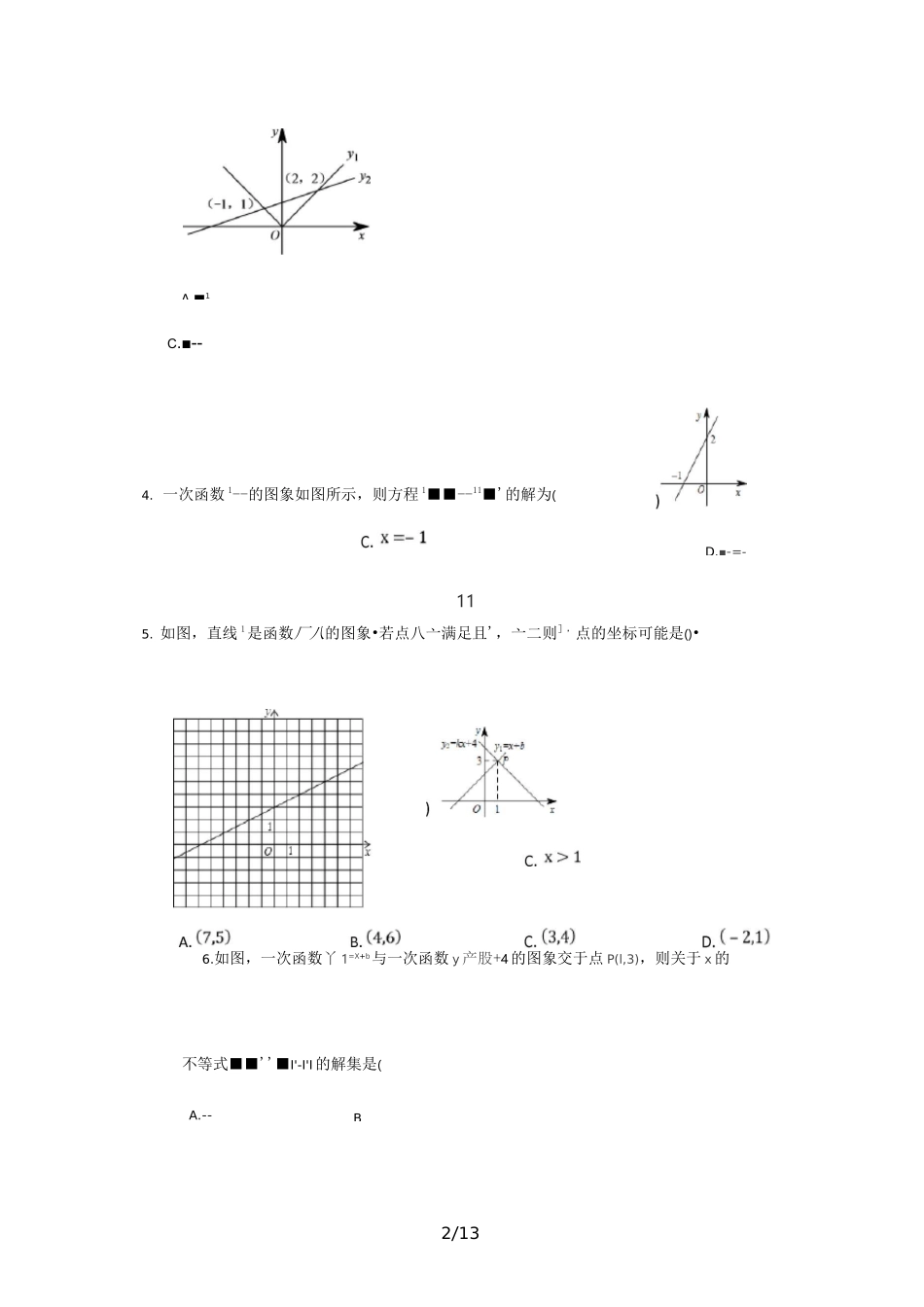
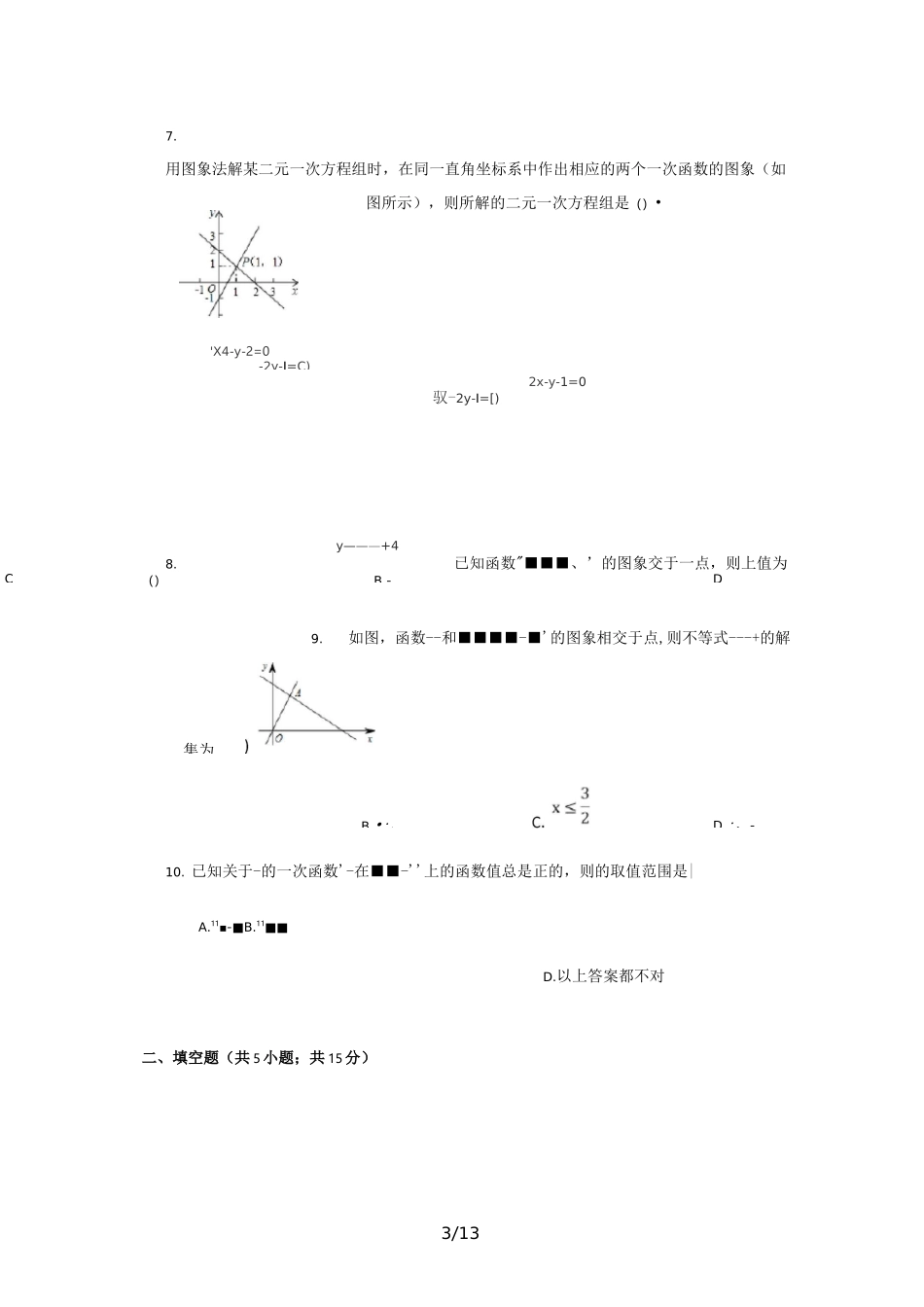
1/13C.最新文件仅供参考已改成word文本方便更改赠人玫瑰,手留余香。一次函数与一元一次不等式训练题及答案一、选择题(共10小题;共30分)1.如图,以两条直线''/的交点坐标为解的方程组是1:12•将一次函数y二戸的图象向上平移2个单位,平移后,若小,则x的取值范围是()D.■--143.如图所示,函数'X和'''-的图象相交于1门,心二两点•当'"■时,'的取值范围是1-12/13BC.■--4.一次函数1--的图象如图所示,则方程1■■--11■'的解为(115.如图,直线1是函数厂八的图象•若点八亠满足且',亠二则],点的坐标可能是()•6.如图,一次函数丫1=X+b与一次函数y产股+4的图象交于点P(l,3),则关于x的不等式■■''■I'-I'I的解集是(A.--A.■1D.■-=-3/13B.-CDB.•:、D.:、-7.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是()•2x-y-1=0驭-2y-I=[)y———+48.已知函数"■■■、’的图象交于一点,则上值为()9.如图,函数--和■■■■-■'的图象相交于点,则不等式---+的解10.已知关于-的一次函数'-在■■-''上的函数值总是正的,则的取值范围是|A.11■-■B.11■■D.以上答案都不对二、填空题(共5小题;共15分)'X4-y-2=0-2y-I=C)集为4/1311.如图,已知函数-■--和'-■+:的图象交于点」’,根据图象可得方程组[x-y=2,:的解是.12.一次函数「二宀1,与''的图象如图,则1--^.的解集13.如图,已知函数I与函数的图象交于点J,,则不等式11的解集是fx+y=15r11,14.方程组::'-的解是'■则直线-■-和-:'-的交点坐标15.观察函数的图象,根据图所提供的信息填空:5/13(1)当匚时,“;(2)当时,堆";(3)当■时,―;(4)当*时厂-.三、解答题(共5小题;共55分)2¥=——x十416.如图,函数--和■的图象相交于点人,(1)求点的坐标;2(2)根据图象,直接写出不等式么%'的解集.17.已知一次函数的图象过点川1",」,求函数表达式并画出它的图象,再利用图象求:(1)当兀为何值时,••1,「:,•1;(2)当—时八的取值范围;(3)当■■-■-:'时,':的取值范围.6/1318.甲、乙两地相距川、汕•,一辆货车和一辆轿车先后从甲地出发驶向乙地•如图,线段;门表示货车离甲地的距离■■■I-与时间!,■之间的函数关系,折线表示轿车离甲地的距离与时间JI之间的函数关系•根据图象,解答下列问题:(1)线段表示轿车在途中停留了h;(2)求线段..V.对应的函数解析式;(3)求轿车从甲地出发后经过多长时间追上货车.19.如图,直线机一'经过点"「,」」.7/13(1)求直线■■I'的解析式;(2)若直线■■I与直线丄相交于点:,求点;的坐标;(3)根据图象,写出关于'、、的不等式丄,.「.-1>的解集.20.如图,在平面直角坐标系中,过点的直线人;与直线爲;相交于点■-,动点沿路线—•运动.8/13(1)求直线-J;的解析式.(2)求一的面积.1(3)当」扛小.的面积是」5的面积的I时,求出这时点的坐标.答第一部分1.C2.B3.D4.C5.B6.C7.D8.B9.A10.A第二部11.fX1\y=-112.x<-213.x<414.(1U)15.(1)'(2)」;(3)V;(4)-16.(1)由题意,得方程组解得9/13第三部分y=2xP2y---x+4.3X=?y=3.f3'■的坐标为3(2)由图象,得不等式的解集为:17.(1)设一次函数的表达式为|把点-VU,」:.■分别代入,J;10/13得/k+b=4.Irk4b=6解得fk-2.(b—2.所以■-,.-二.一次函数-”-二的图象如图所示.由图可知,直线''<'■'与-轴交于「丨『点,当<-J时,•;」:;(2)当时,_4uy<:2.(3)当一、二时,二―飞.18.(1):1■'(2)设线段*对应的函数解析式是':.v1)(2.530),1:(4.5.300)/80=2.5k+b,1^00=4.5k+h.k=110,b=-195.故线段•厂对应的函数解析式是-2、:'''-!■A•11/13(3)设线段肿对应的函数解析式是"'',vA(5±300),:*k|二60(y=110x-1线段幕对应的函数解析式是'.解方程组"「展M二39(y=234.「I"(小时).答:轿车从甲地出发后经过“小时追上货车.19.(1)直线小一卜经过点,」门,[5k+h=①所以m(k==-L解方程得"二二',直线5的解析式为"''.(2)直线-->■-I与直线人;相交于点:,fy=-x+5,'■解方程组〔;-二一-(x=3,得'■点:的坐标为.(3)当'■-时•直线■'■-1位于直线■'、上方.不等式和的解集为■<--.20...