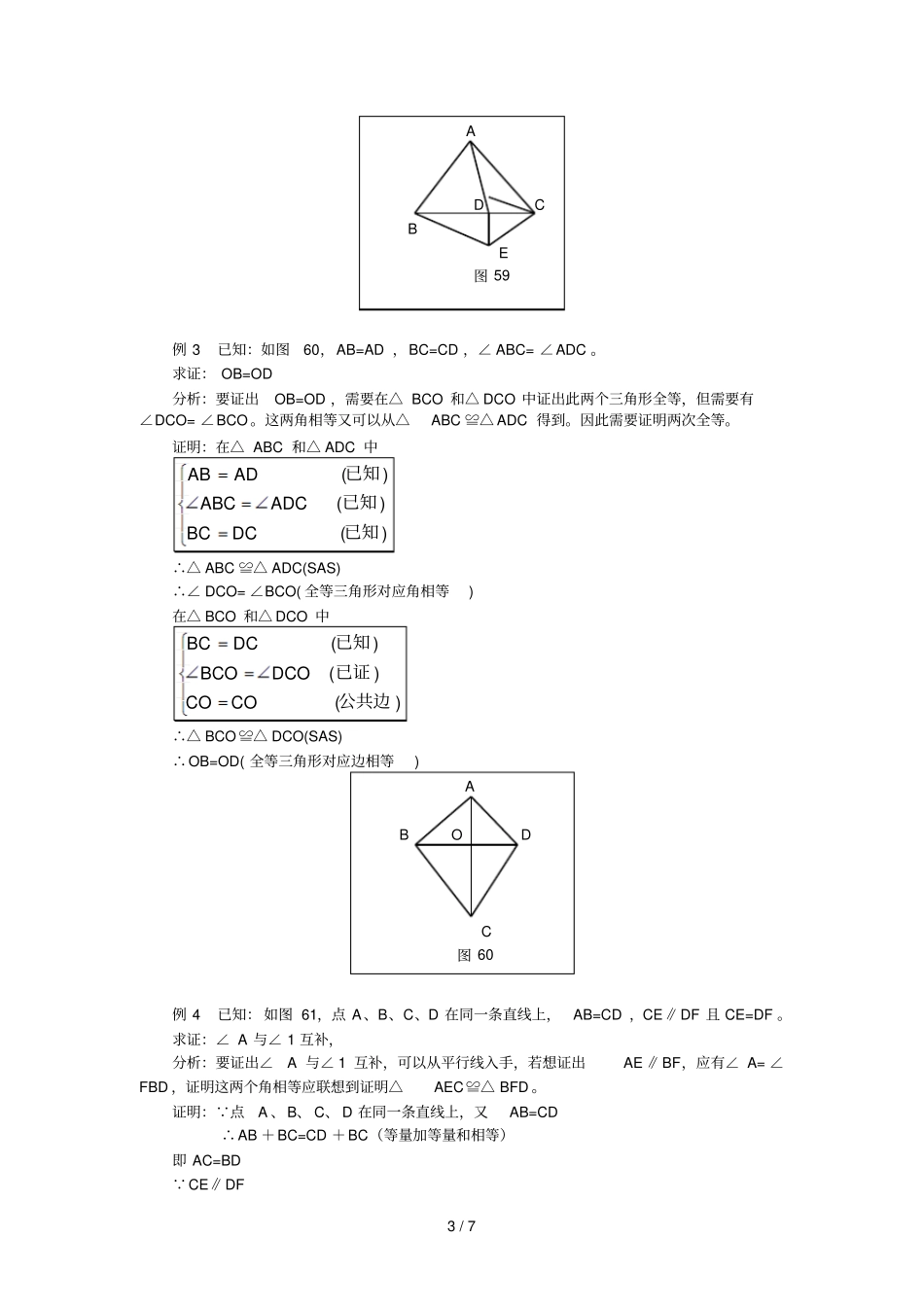
1/7三角形全等的判定(一)一、教学目的和要求理解并掌握三角形全等的判定公理1,能准确找到判定公理1的条件,并熟练运用。二、教学重点和难点重点:能准确应用判定公理1的条件。难点:在条件不明显的情况下找出较为陈蔽的条件,从而运用判定公理1。三、教学过程(一)复习、引入提问:1.上一节课已经学习了判定公理1,请同学们回忆并叙述(边、角、边)2.证明三角形全等时,怎样找到公理1的条件?(两条对应边及夹角相等)3.三角形全等的性质是什么?(对应边相等,对应角相等)练习:1.已知:如图57,DC⊥CA,DA⊥CA,CD=AB,CB=AE求证:△BCD≌△EABDECBA图57证明: DC⊥CA,EA⊥CA(已知)∴∠C=∠A=90°(垂直定义)在△BCD≌△EAB中CDABCACBAE()()()已知已证已知∴△BCD≌△EAB(SAS)上面这个练习同学们能较快作出来,因为所给条件比较明显。但有些题目已知中隐含着证明全等的条件,需要用以前学过的知识。比如:平行线性质;垂直定义;等量加等量和相等;或者由一次全等推出对应边相等、对应角相等,再由此证出所需三角形全等,也就是要证两次全等。下面看几个例题,加强这方面训练。(二)新课例1已知:如图58,EB⊥CD,BE=DE,AE=CE,求证:DABC分析:由已知条件,BE=DE,AE=CE,已有两组对应边相等,再找夹角相等就可以了,可以根据已知BE⊥CD,推出∠BEC=∠DEA=90°,由此可以证出△BEC≌△DEA。由全2/7等三角形知对应角相等,则∠B=∠D,再由∠B+∠C=90°可推出∠D+∠C=90°,进而可证明DA⊥BC。BFACED图58证明:延长DA与BC交于F点. BE⊥CD∴∠BEC=∠DEA=90°(垂直定义)在△BEC和△DEA中BEDEBECDEACEAE()()()已知已证已知∴△BEC≌△DEA(SAS)∴∠B=∠D(全等三角形对应角相等) ∠B+∠C=90°(三角形内角和为180°)∴∠D+∠C=90°(等量代换)∴∠CFD=90°(三角形内角和定理)即DABC(垂直定义)例2已知:如图59,△ABC和△DEC都是等边三角形,各角都等于60°。求证:AD=BE分析:可先证△ACD与△BCE全等。已知AC=BC,CD=CE,显然应设法证夹角∠ACD与夹角∠BCE相等。证明: △ABC△BCE都是等边三角形(已知)∴∠ACB=∠DCE=60°(等边三角形各角等于60°)∴∠ACB-∠DCB=∠DCE-∠DCB(等量减等量,差相等)即∠ACD=∠BCE在△ADC与△BEC中ACBCACDBCECDCE(()()等边三角形定义已证等边三角形定义)∴△ADC≌△BEC(SAS)∴AD=BE(全等三角形对应边相等)3/7ADCBE图59例3已知:如图60,AB=AD,BC=CD,∠ABC=∠ADC。求证:OB=OD分析:要证出OB=OD,需要在△BCO和△DCO中证出此两个三角形全等,但需要有∠DCO=∠BCO。这两角相等又可以从△ABC≌△ADC得到。因此需要证明两次全等。证明:在△ABC和△ADC中ABADABCADCBCDC()()()已知已知已知∴△ABC≌△ADC(SAS)∴∠DCO=∠BCO(全等三角形对应角相等)在△BCO和△DCO中BCDCBCODCOCOCO()()()已知已证公共边∴△BCO≌△DCO(SAS)∴OB=OD(全等三角形对应边相等)ABODC图60例4已知:如图61,点A、B、C、D在同一条直线上,AB=CD,CE∥DF且CE=DF。求证:∠A与∠1互补,分析:要证出∠A与∠1互补,可以从平行线入手,若想证出AE∥BF,应有∠A=∠FBD,证明这两个角相等应联想到证明△AEC≌△BFD。证明: 点A、B、C、D在同一条直线上,又AB=CD∴AB+BC=CD+BC(等量加等量和相等)即AC=BD CE∥DF4/7∴∠ACE=∠D(两直线平行同位角相等)在△AEC≌△BFD中ACBDACEDCEDF()()()已证已证已知∴△ACE≌△BDF(SAS)∴∠A=∠FBD(全等三角形对应角相等)∴AE∥BF(同位角相等,两直线平行)∴∠A与∠1互补(两条直线平行,同旁内角互补)EF1ABCD图61(三)巩固练习1.已知:如图62,AC、BD互相平分于O。DCAD1OEFABB2C图62图63求证:△AOB≌△COD。2.已知:如图63,点A、E、F、C在同一条直线上,AD=CB,∠1=∠2,AE=CF。求证:∠B=∠D(四)小结1.在已知中证明三角形全等条件不明显时,应分析在已知中已满足了哪些条件,还差哪些条件,然后用以前学过的知识将证明全等的条件找全,然后按步骤证明三角形全等。2.在题目的求证中不是直接求证三角形全等,而是求证边相等或角相等,此时可以联系三角形全等的性质、分析出先证哪两个三角形全等,再进一步推出对应边或对应角相等。(五)作...