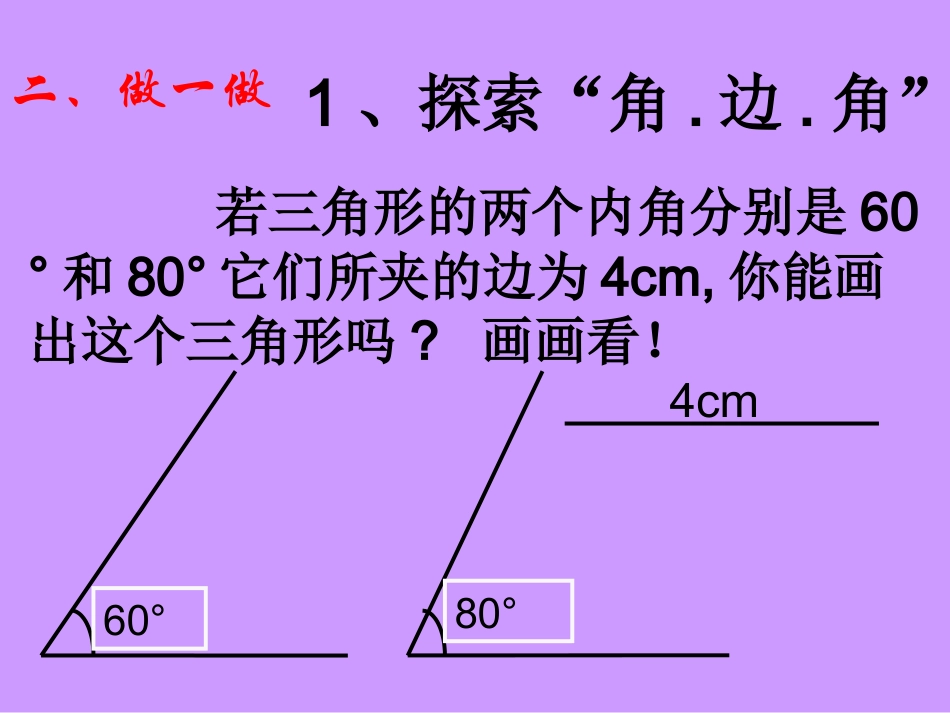
探索三角形全等的条件(第二课时)灵武市回民中学刘明雄一、创设问题我们知道:如果给出一个三角形三条边的长度,那么得到的三角形都是全等.如果已知一个三角形的两角及一边,那么有几种可能的情况呢?每种情况下得到的三角形都全等吗?1、角.边.角;2、角.角.边二、做一做1、探索“角.边.角”;若三角形的两个内角分别是60°和80°它们所夹的边为4cm,你能画出这个三角形吗?画画看!4cm60°80°你画的三角形与同伴画的一定全等吗?剪下来比一比。60°80°2、思考交流总结•1、画△ABC,使∠A=500,B=30∠0,AB=2cm.观察比较发现什么?•2、你还能改变数据构造这样的三角形吗?•3、由此你能得出什么结论?•两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”3、探索“角.角.边”若三角形的两个内角分别是60°和40°,且40°所对的边为4cm,你能画出这个三角形吗?60°40°60°40°分析:这里的条件与1中的条件有什么相同点与不同点?你能将它转化为1中的条件吗?80°画一画,比一比,你们又发现什么?两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”4、认识理解结论•1、你将我们所得到的两个结论翻译成图形语言和几何符合语言:三角形全等的判定公理三角形全等的判定公理22:∵:∵∠∠B=B=∠∠EE,,BC=EFBC=EF,,∠∠C=C=∠F∠F∴∴ΔΔABCABC≌≌DEFDEF((ASAASA))三角形全等的判定公理三角形全等的判定公理33:∵:∵∠∠B=B=∠∠EE,,∠∠C=∠FC=∠F,,AC=DAC=DFF∴∴ΔΔABCABC≌≌DEFDEF((AASAAS))AABBCCDDEEFFAABBCCDDEEFF三、练一练:1、完成下列推理过程:在△ABC和△DCB中,∠ABC=DCB∠∵BC=CB∴△ABCDCB≌△()ASAABCDO1234()公共边∠2=1∠AAS∠3=∠4∠2=∠1CB=BC2、请在下列空格中填上适当的条件,使△ABCDEF≌△。在△ABC和△DEF中∵∴△ABCDEF≌△()ABCDEFSSSAB=DEBC=EFAC=DFASA∠A=D∠AB=DE∠B=DEF∠AC=DF∠ACB=F∠AAS∠B=DEF∠BC=EF∠ACB=F∠BC=EF四、想一想:如图,O是AB的中点,∠A=B∠,△AOC与△BOD全等吗?为什么?ABCDO我的思考过程如下:两角与夹边对应相等∴△AOCBOD≌△五、练一练:DCBA1、在△ABC中,AB=AC,AD是边BC上的中线,证明:∠BAD=CAD∠证明:∵AD是BC边上的中线∴BD=CD(三角形中线的定义)在△ABD和△ACD中)AD(AD)CD(BD)AC(AB公共边已证已知∴△ABDACD≌△(SSS)∴∠BAD=CAB∠(全等三角形对应角相等)AD是∠BAC的角平分线。求证:BD=CD证明:∵AD是∠BAC的角平分线(已知)∴∠BAD=∠CAD(角平分线的定义)∵AB=AC(已知)∠BAD=∠CAD(已证)AD=AD(公共边)∴△ABDACD≌△(SAS)∴BD=CD(全等三角形对应边相等)2、若△ABC中,∠A=30°,∠B=70°,AC=5cm,DEF△中∠D=70°F∠=80°,DF=5cm,那么△ABC与△DEF全等吗?为什么?3、如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?如果可以,带哪块去合适?你能说明其中理由吗?两角和它们的夹边对应相等的两个三角形全等。(1)两角和它们的夹边对应相等的两个三角形全等.简写成“角边角”或“ASA”.(2)两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.知识要点:(3)探索三角形全等是证明线段相等(对应边相等),角相等(对应角相等)等问题的基本途径。数学思想:要学会用分类的思想,转化的思想解决问题。布置作业•上交作业:•P104-------第1、4题•家庭作业:•1、P104-----第2、3题•2、预习下一课时内容。