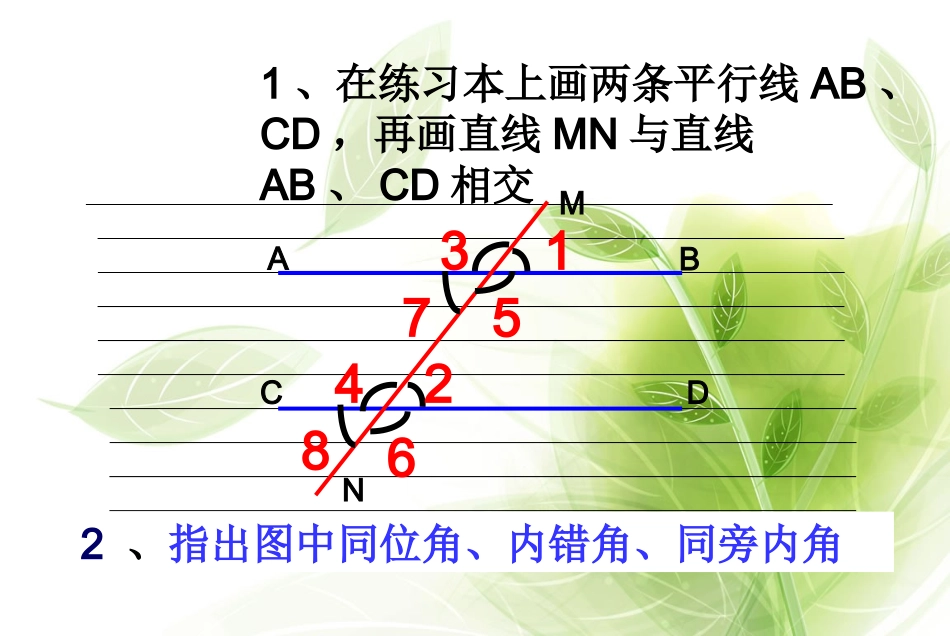
5.3.1平行线的性质复习(1)∵∠4=___∠∴ab∥()(2)∵∠=2∠∴ab∥()12同位角相等,两直线平行内错角相等,两直线平行cb4321a根据右图回答下列问题ABCDMN1、在练习本上画两条平行线AB、CD,再画直线MN与直线AB、CD相交2、指出图中同位角、内错角、同旁内角1328457612753、将上图按照如下方式剪开,并分别把剪开得到的每对同位角、内错角重叠,你发现了什么?两直线平行同位角相等12754、将上图按照如下方式剪开,并分别把剪开得到的每对同位角、内错角重叠,你发现了什么?两直线平行同旁内角____互补5、你能根据”两直线平行,同位角相等”,说明“两直线平行,内错角相等”成立的理由吗?abc127解:∵ab∥(已知)∴∠1=2∠(两直线平行,内错角相等)又∵∠1=7∠(对顶角相等)∴∠2=7∠(等量代换)两直线平行,内错角相等平行线的性质两直线平行,同位角相等;两直线平行,内错角相等;两直线平行同旁内角互补。abc1275例1已知:直线a∥b,c∥d,∠1=115°,求∠2与∠3的度数解:∵ab∥∴∠2=∠1=115°∵cd∥∴∠3=∠2=115°(两直线平行,内错角相等)(已知)(已知)(两直线平行,内错角相等)123abcd1.如图1若ABCD,∥则下列结论中①∠B=23=A3=B∠②∠∠③∠∠④B+∠BCD=180°∠正确的是()ABCD①②①③①④③④D×√×√练习一2.如图2,若ABED,BCFE,∥∥则∠B+E=____∠123ABCDE1ABCDEF2180°1.如图1,AD∥BC,∠A=∠C.试说明AB∥DCAEFCBD练习二2.如图2,已知AB∥CD,求∠A+∠B+∠ACB的度数.ABCD2112课堂小结:通过本节课的学习,你有什么感悟(1)平行线的三条性质(2)利用平行线的三条性质解计算题和简单的解答题(3)学无止境乘胜前进?课堂小结练习例题结论归纳探究复习题平行线的性质