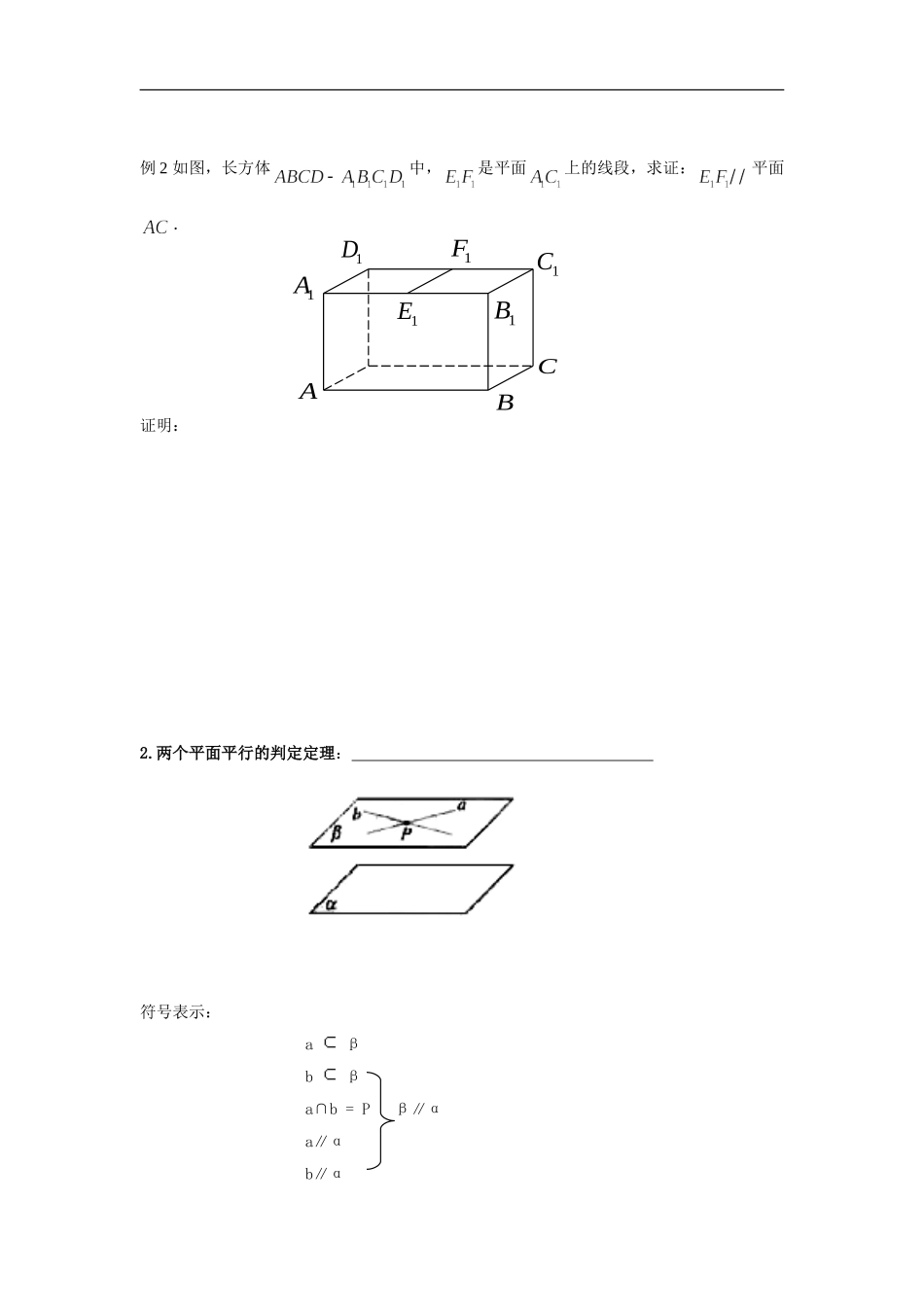
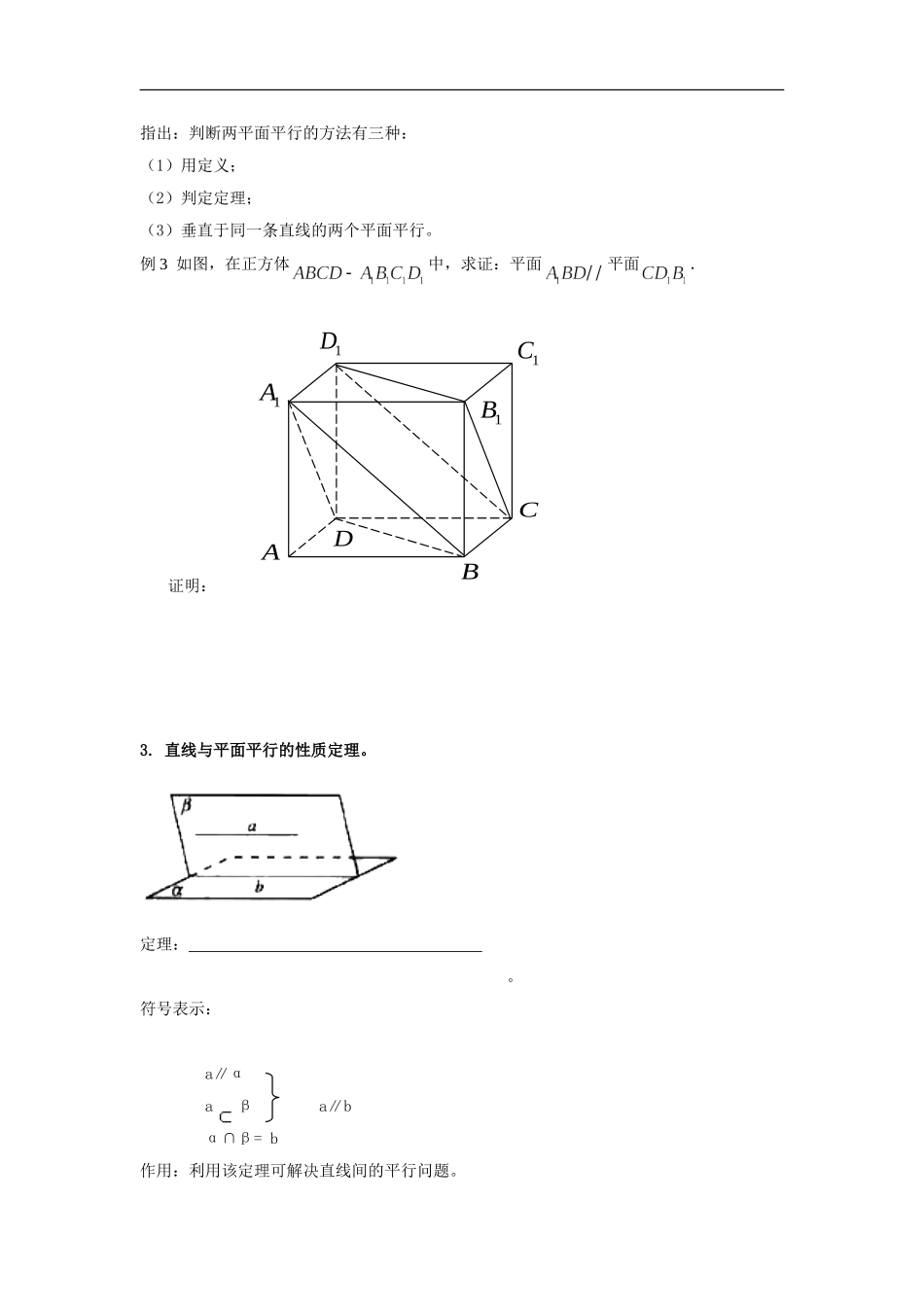
2.2《直线、平面平行的判定与性质》导学案【学习目标】(1)理解并掌握直线与平面平行的判定定理;理解并掌握两平面平行的判定定理。(2)进一步培养学生观察、发现的能力和空间想象能力;(3)掌握直线与平面平行的性质定理及其应用;(4)掌握两个平面平行的性质定理及其应用。【导入新课】观察身边的实物,如教材第55页观察题:封面所在直线与桌面所在平面具有什么样的位置关系?如何去确定这种关系呢?这就是我们本节课所要学习的内容。新授课阶段1.直线与平面平行的判定定理:简记为:线线平行,则线面平行。符号表示:aαbβ=>a∥αa∥b例1如图,已知点是平行四边形所在平面外的一点,,分别是,上的点且,求证:平面.证明:αaαab例2如图,长方体中,是平面上的线段,求证:平面.证明:2.两个平面平行的判定定理:符号表示:aβbβa∩b=Pβ∥αa∥αb∥αABC1A1D1B1C1F1E指出:判断两平面平行的方法有三种:(1)用定义;(2)判定定理;(3)垂直于同一条直线的两个平面平行。例3如图,在正方体中,求证:平面平面.证明:3.直线与平面平行的性质定理。定理:。符号表示:a∥αaβa∥bα∩β=b作用:利用该定理可解决直线间的平行问题。1D1A1C1BABDC4.两个平面平行的性质定理定理:。符号表示:α∥βα∩γ=aa∥bβ∩γ=b指出:可以由平面与平面平行得出直线与直线平行例4如图,线段,所在直线是异面直线,,,,分别是线段,,,的中点.(1)求证:共面且面,面;(2)设,分别是和上任意一点,求证:被平面平分.证明:课堂小结1、面面平行的定义;2、面面平行的判定定理和性质定理;3、面面平行判定定理的应用:要证面面平行,只要证线面平行,而要证线面平行,只要证线线平行。在立体几何中,往往通过线线、线面、面面间的位置关系的转化使问题得到解决。作业AEHCFBGDMPQN见同步练习部分拓展提升1.三棱锥中,,截面与、都平行,则截面的周长是()A.B.C.D.周长与截面的位置有关2.已知:,,,则与的位置关系是()A.B.C.、相交但不垂直D.、异面3.为所在平面外一点,平面平面,交线段,,于,,则。4.如图,在四棱锥中,是平行四边形,,分别是,的中点。求证:平面。5.如图,已知点是平行四边形所在平面外的一点,、分别是、上的点且,求证:平面。APDMNBCPEACBDF参考答案新授课阶段1.直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。简记为:线线平行,则线面平行。符号表示:aαbβ=>a∥αa∥b例1证明:连结并延长交于.连结,,,又由已知,.由平面几何知识可得,又,平面,平面.例2证明:如图,分别在和上截取,,连接,,.αaαabABCD1A1D1B1C1F1E长方体的各个面为矩形,平行且等于,平行且等于,故四边形,为平行四边形.平行且等于,平行且等于.平行且等于,平行且等于,四边形为平行四边形,.平面,平面,平面.2.两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。符号表示:aβbβa∩b=Pβ∥αa∥αb∥α指出:判断两平面平行的方法有三种:(1)用定义;(2)判定定理;ABCD1A1D1B1C1F1EEF(3)垂直于同一条直线的两个平面平行。例3证明:四边形是平行四边形.3.直线与平面平行的性质定理。一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。简记为:线面平行则线线平行。4.两个平面平行的性质定理如果两个平面同时与第三个平面相交,那么它们的交线平行。例41D1A1C1BABDCAEHCFBGDMPQN证明:(1),,,分别是,,,的中点.,,,.因此,,,,共面.,平面,平面,平面.同理平面.(2)设平面=,连接,设.所在平面平面=,平面,平面,.是是的中位线,是的中点,则是的中点,即被平面平分.拓展提升1.B.2.A.3.4.证明:如图,取的中点,连接,,分别是,的中点,,,可证明平面,平面.又,平面平面,又平面,平面.5证明:连结并延长交于.连结,,,又由已知,.由平面几何知识可得,又,平面,平面.APDMNBCE