讲课第六章《实数》教学课件VIP免费

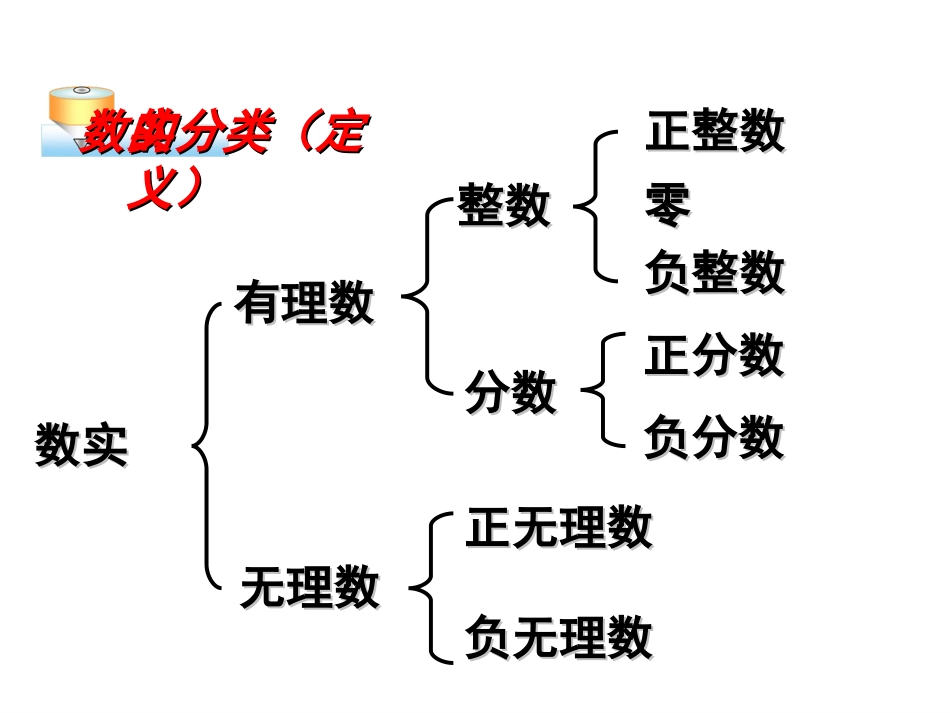
6.3实数有理数包括哪几类？有理数包括哪几类？有理数整数分数有限小数,87,52,6.0无限循环小数3.031,128574.073,4142.122599210.123,1415926.3012012001200.1无限不循环小数无理数无理数实数实数实数实数有理数有理数无理数无理数整数整数分数分数正无理数正无理数负无理数负无理数正整数正整数零零负整数负整数正分数正分数负分数负分数实数的分类（定实数的分类（定义）义）实数实数正实数正实数负实数负实数正有理数正有理数正无理数正无理数负有理数负有理数负无理数负无理数正整数正整数零零负整数负整数正分数正分数负分数负分数实数的分类（性实数的分类（性质）质）…………把下列各数分别填在相应的集合中：把下列各数分别填在相应的集合中：382025722331415926.3）之间依次多一个（两个133131131113.0543.0213有理数集合有理数集合无理数集合无理数集合3820257221415926.3543.021333练习练习００１１２２３３４４实数与数轴实数与数轴直径为１个单位长度的圆从原点沿数直径为１个单位长度的圆从原点沿数轴向右滚动一周，圆上的一点Ｏ由原点到轴向右滚动一周，圆上的一点Ｏ由原点到达点Ｏ′，点Ｏ′的坐标是多少？达点Ｏ′，点Ｏ′的坐标是多少？ＯＯＯ′Ｏ′从图中可以看出，从图中可以看出，OO′OO′的长是这的长是这个圆的周长个圆的周长ππ，所以，所以O′O′的坐标是的坐标是ππ．．-2-2-1-1001122以单位长度为边长画一个长方以单位长度为边长画一个长方形，以原点为圆心，正方形对角线为半径形，以原点为圆心，正方形对角线为半径画弧，与正半轴的交点就表示，与画弧，与正半轴的交点就表示，与负半轴的交点就表示。负半轴的交点就表示。22梳理梳理当数从有理数扩充到实数以后，实数当数从有理数扩充到实数以后，实数与数轴上的点就是一一对应的，即每一个实数与数轴上的点就是一一对应的，即每一个实数都可以用数轴上的一个点来表示；反过来，数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都表示一个实数。轴上的每一个点都表示一个实数。事实上，每一个无理数都可以用数轴事实上，每一个无理数都可以用数轴上的一个点表示出来。这就是说，数轴上的点上的一个点表示出来。这就是说，数轴上的点有些表示有理数，有些表示无理数。有些表示有理数，有些表示无理数。当数从有理数扩充当数从有理数扩充到实数以后，有理数关于相到实数以后，有理数关于相反数和绝对值的意义同样适反数和绝对值的意义同样适合于实数。合于实数。梳理梳理-π-π的相反数是的相反数是；；00的相反数是的相反数是；；的相反数是的相反数是；；220，，，，，，22ππππ0000数数aa的相反数是的相反数是-a-a，这里，这里aa表示任意一个实表示任意一个实数。数。一个正实数的绝对值是它本身；一个一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数；负实数的绝对值是它的相反数；00的绝对值是的绝对值是00。。在实数范围内，相反数、倒数、绝在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。倒数、绝对值的意义完全一样。（1）a是一个实数，它的相反数为，绝对值为；（2）如果a0，那么它的倒数为.aaa1填空填空２、的相反数是２、的相反数是，绝对，绝对值是值是．．3３、绝对值等于的数是３、绝对值等于的数是，，的平方是的平方是．．75４、比较大小：－７４、比较大小：－７43１、正实数的绝对值是１、正实数的绝对值是，，０的绝对值是０的绝对值是，负实数的绝对值是，负实数的绝对值是..它本身0它的相反数335755、一个数的绝对值是，则这个、一个数的绝对值是，则这个数是数是..2p2p例1：(1)分别写出-,的相反数;63.14例题例题例例11（（22）的绝对）的绝对值；值；364求464344643解：解：（（33）已知一个数的绝对值是）已知一个数的绝对值是，求这个值。，求这个值。333解：解：33∴∴绝对值为的数是或绝对值为的数是或。。333练习:求下列各数的相...