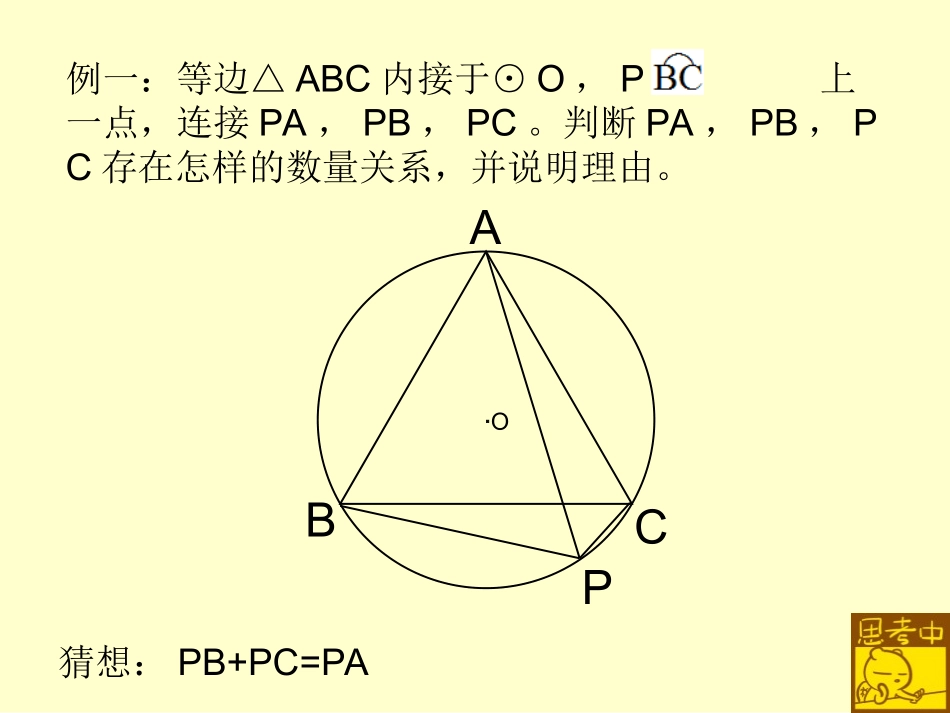
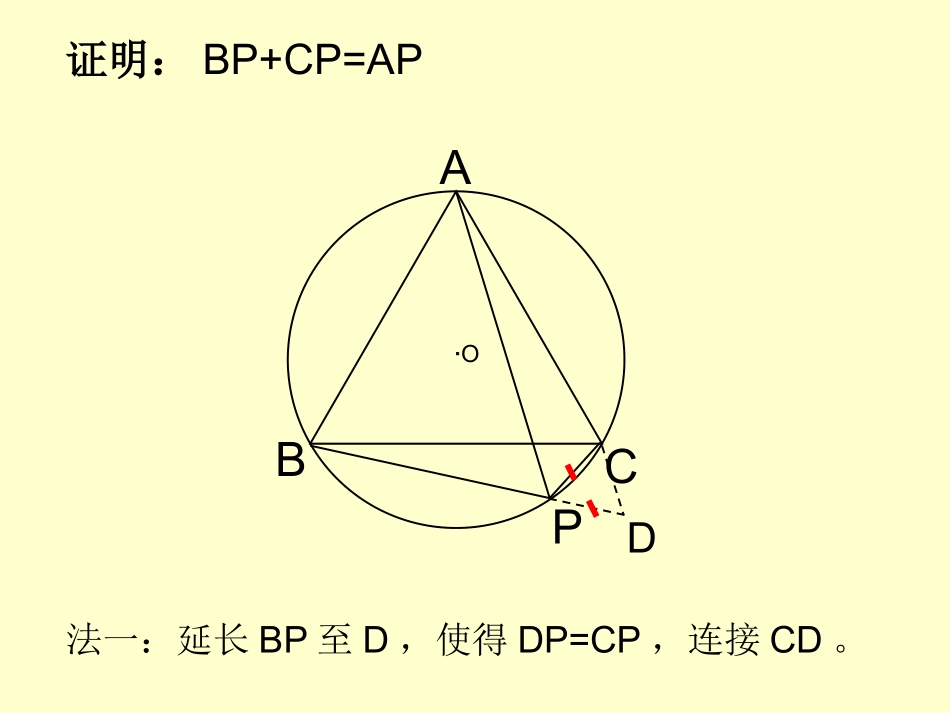
与圆相关的计算与证明——探索线段之间的数量关系初三年级组刘芳例一:等边△ABC内接于⊙O,P为上一点,连接PA,PB,PC。判断PA,PB,PC存在怎样的数量关系,并说明理由。ABCP·O猜想:PB+PC=PAABCPD·O法一:延长BP至D,使得DP=CP,连接CD。证明:BP+CP=APABCPD·O法一:等边△CDP→BCDACP△≌△ABCPD·O法二:延长PB至D,使得BD=CP,连接AD。ABCPD·O法二:△BCDACP→ADP≌△△为等边三角形。想一想:以上两种方法哪种更简单?法一:等边△CDP→BCDACP→BD=AP△≌△法二:△BCDACP→≌△等边△ADP→DP=APABCPDABCPD·O·OABCPD·O法三:在AP上取点D,使得DP=CP,连接CD。法三:等边△CDP→BCPACD△≌△。ABCPD·OABCPD·O法四:在AP上取点D,使得AD=CP,连接BD。法四:△ABDACP→BDP≌△△为等边三角形。ABCPD·OABCPDE·O法五:过A点作ADBP⊥于点D,AEPC⊥于点EABCPDE·O法五:△ABDACE≌△、△ADPADE→≌△BP+CP=2DP想一想:以上两种方法哪种更简单?法三:等边△CDP→ADCBCP→AD=BP△≌△法四:△ADBACE≌△、△ADPADE≌△→BP+CP=2DPEABCPD·OABCPD·O练习:等腰RtABC△内接于⊙O,∠BAC=90°,AB=AC,P为上一点,连接PA,PB,PC。判断PA,PB,PC存在怎样的数量关系,并说明理由。BCPA·OBCPAD·O法一:延长PB至D,使得BD=CP,连接AD。证明:BP+CP=AP2BCPAD·OBCPADE·O法二:过A点作ADBP⊥于点D,AEPC⊥于点E。BCPADE·O法二:过A点作ADBP⊥于点D,AEPC⊥于点E。想一想:以上两种方法哪种更简单?BCPADE·OBCPAD·O小结:在处理有关线段关系过程的问题中,我们可以通过截长补短构建新的特殊三角形及全等三角形达到解决问题的目的。还可以根据已知条件中的角平分线过角平分线上的点向两边作垂线,构建全等三角形及特殊三角形来解决问题。作业:1:完成我们今天所学题目的解答过程(一种方法即可)。2:(选做)思考:等腰△ABC内接于⊙O,∠BAC=120°,AB=AC,P为上一点,连接PA,PB,PC。判断PA,PB,PC存在怎样的数量关系,并说明理由。BCPA·O知识像一艘船让它载着我们驶向理想的……