7.1简单几何体的侧面积VIP免费

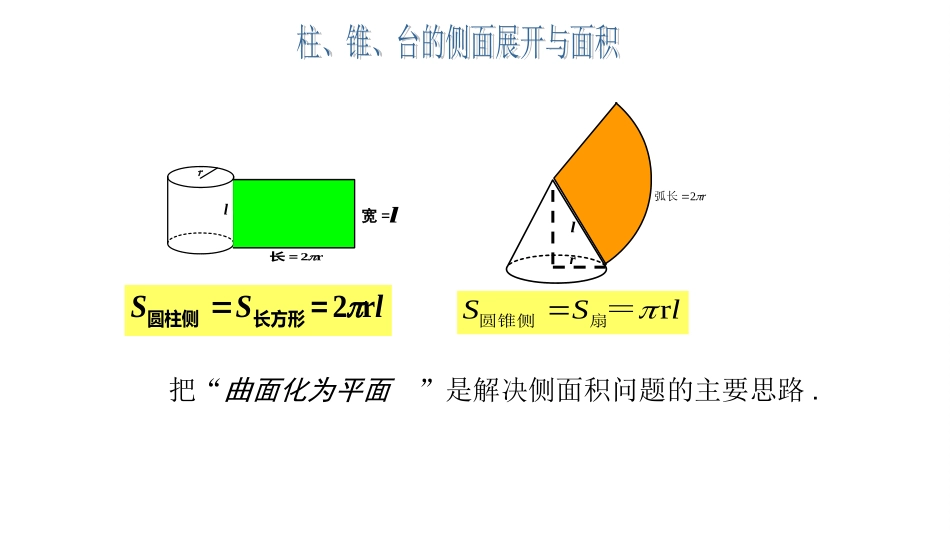
rlr2长＝宽=llSSr2＝长方形圆柱侧rl把“曲面化为平面”是解决侧面积问题的主要思路.rSSl圆锥侧扇＝r2弧长rlr2长＝宽=llSSr2＝长方形圆柱侧rlh'h'h'h'12Sch正棱锥侧1+2Scch正棱台侧rSSl圆锥侧扇＝2r弧长＝SSch矩形直棱柱侧Ch01021r2rlABs圆台侧面积公式推导1212)SSSrrl圆台侧扇环=S（1122OArOBr2xlr1s=21sxr12rxxlr即121lrxrr得12,,SAxSBlxSOASOB设则由△△得s011r2rl02AB12SSrrl圆台侧扇环＝xrlS2＝圆柱侧rlS圆锥侧rrr21lrrS)21（圆台侧rrr21,0圆柱、圆锥、圆台的侧面积公式之间圆柱、圆锥、圆台的侧面积公式之间有何关系有何关系,,如何转化？如何转化？埃及胡夫金字塔大约建于公元前2580年，其形状为正四棱锥，金字塔高约h米,底面边长约a米,试用a、h表示这座金字塔的侧面积是多少？典例分析埃及胡夫金字塔大约建于公元前2580年，其形状为正四棱锥，金字塔高约h米,底面边长约a米,试用h、a表示这座金字塔的侧面积是多少？典例分析解：如图，在中，，，，SOERthSO2aOE90SOE所以，由于，422ahSEBCSE所以4212122ahaSEBCSSBC因为正四棱锥的四个侧面等腰三角形都相等，所以2222144424SBCaSSahaha侧答：这座金字塔的侧面积为平方米.224aha设顶点S在底面是垂足为点O，过点O作OE，连接SE.BC解：解：ABCDOESh2a课堂练习：2.3,6正四棱台的上、下两底面边长分别是，其侧面积等于两底面积之和，则其斜高是多少？52h..1，求表面积，底面边长为已知正六棱柱的高为ah2336aah1、圆柱、圆锥、圆台、直棱柱、正棱锥、正棱台的侧面积公式不需要记忆，但是同学们需要真正理解并会应用.课堂小结：3、掌握了立体几何问题化为平面几何问题的数学思想和类比的数学思想方法.2、应用侧面积公式解决有关问题.2.书面作业：课本P51第7、10题.作业：1.阅读课本.3.拓展作业：胡夫金字塔包含许多数学问题，大家上网查询，体会胡夫金字塔中蕴含的数学魅力.2.书面作业：课本P51第7、10题.谢谢大家！例.一个正三棱台的上下底面边长分别为3cm和6cm，高是cm,求三棱台的侧面积.23解：1OOABC1A1B1CD1DE如图，分别是上、下底面中心,则OO,1231OO连接并延长交于，连接并延长交于11OA11CB1DAOBCD过作于，在中1DADED1EEDDRt12311OOED11ODDOOEDODE2336233132232232211DEEDDD所以21'cm232721DDccS正三棱台侧答：三棱台的侧面积为22327cm巩固提高拓展如图，圆锥的底面圆半径5cm，母线PB=10cm，AB为底面直径，C为PB的中点，现有一只蚂蚁，沿圆锥表面从A爬到C，它至少爬多远?请说出你的解题方案.10cmABPC.圆台的上、下底半径分别是10cm和20cm，它的侧面展开图的扇环的圆心角是180o，那么圆台的侧面积是多少？(结果中保留π)BAO2s2010SO1解：如图，设上底面周长为.c因为扇环的圆心角是，所以180SAc又因为，所以，同理20102c20SA40SB所以.20SASBAB.600202010221cmABrrS答：圆台的侧面积为.6002cm巩固提高